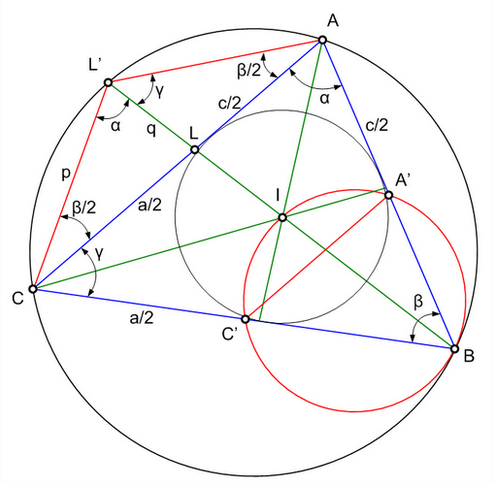
Пусть точка I – центр вписанной окружности треугольника ABC,
точки А’ и C’ - середины сторон с и а соответственно.
Продолжим биссектрису BL до пересечения с описанной окружностью
в точке L’ и проведем отрезки CL’ и AL’.
Пусть p=|CL’|, q=|LL’|, f=|BL|.
Биссектриса CI делит биссектрису BL на отрезки LI/BI=CL/CB= 1/2,
т.е. |IL|=f/3. (1)
Углы BAC и BLC равны как опирающиеся на одну хорду CB:
^BAC=^BLC=α.
Так же ^L’CA=^L’BA= β/2.
Тогда ΔСLL’ подобен ΔABL. Следовательно,
c/(c/2)=p/q, т.е. q=p/2. (2)
Точка L’ делит пополам дугу AL’C, следовательно
p=((a/2+c/2)/2)/cos(β/2)=(a+c)/(4cos(β/2)), (3)
Тогда q=(a+c)/(8cos(β/2)) (4)
Найдем длину биссектрисы f.
По теореме косинусов для ΔBCL:
(a/2)^2=f^2+a^2 – 2af*cos(β/2) (5)
для ΔABL:
(с/2)^2=f^2+с^2 – 2сf*cos(β/2) (6)
Вычитая (5) из (6), имеем:
¼ (c^2-a^2)=c^2-a^2 – 2f(c-a)cos(β/2)
и после преобразований:
f=3(a+c)/(8cos(β/2)). (7)
Следовательно, с учетом (1):
|IL|=(a+c)/(8cos(β/2)). (8)
Итак, из (1), (4) и (8) следует, что
q=|IL| и |IL’|=q+|IL|=|BI|= ½ |BL’|. (9)
Таким образом, при гомотетии с центром в вершине B и коэффициентом
1/2 ΔABC переходит в ΔA’BC’, описанная окружность ΔABC в описанную
окружность ΔA’BC’, точка L’ в точку I, лежащую в силу (9)
на описанной окружности ΔA’BC’, что и требовалось доказать.