EB/EC=AB/AC=c/b, следовательно, EB/(EB+a)=c/b;
b*EB=c*EB+ac;
EB=ac/(b-c);
EL=EB+BL=ac/(b-c)+ac/(b+c)=2abc/(b^2-c^2)
AL=(bc-BL*CL)^0,5=
=(bc-(a^2*bc)/(b+c)^2)^0,5=(bc((b+c)^2-a^2)/(b+c)^2)^0,5=
=(bc(b+c+a)(b+c-a))^0,5/(b+c);
OL=AL*BL/(BL+c)=
=((bc-(a^2*bc)/(b+c)^2)^0,5)*(ac/(b+c))/((ac/(b+c)+c)=
=((bc-(a^2*bc)/(b+c)^2)^0,5)*(a/(a+b+c))=
=a(bc(b+c+a)(b+c-a))^0,5/((b+c)(a+b+c)).
AE || OM. Из подобия треугольников AEL и OML следует:
ML/EL=OL/AL;
ML=EL*OL/AL=
=(2abc/(b^2-c^2))*(a(bc(b+c+a)(b+c-a))^0,5/((b+c)(a+b+c)))/
/((bc(b+c+a)(b+c-a))^0,5/(b+c))=
=2bca^2/((b^2-c^2)(a+b+c)).
Соответственно,
MB=ML-BL=2bca^2/((b^2-c^2)(a+b+c)) - ac/(b+c)=
=a(2abc-c(b-c)(a+b+c))/((b^2-c^2)(a+b+c));
MC=ML+LC=2bca^2/((b^2-c^2)(a+b+c))+ ab/(b+c)=
=a(2abc+b(b-c)(a+b+c))/((b^2-c^2)(a+b+c)).
После преобразований:
MB=ac(b+c)(a+c-b)/((b^2-c^2)(a+b+c));
MC=ab(b+c)(a+b-c)/((b^2-c^2)(a+b+c)).
MB*MC=bca^2(b+c)^2(a+c-b)(a+b-c)/((b^2-c^2)(a+b+c))^2=
=bca^2*(a+c-b)(a+b-c)/((b-c)^2*(a+b+c)^2) (I)
Рассмотрим теперь треугольник AML.
Eго высота AH=h=½ ((a+b+c)(a+b-c)(a-b+c)(-a+b+c))^0,5/a
Его площадь:
S=½ h*LM=½ OM*AL.
Отсюда:
OM=h*LM/AL=
=h*2bca^2/((b^2-c^2)(a+b+c))/(bc-(a^2*bc)/(b+c)^2)^0,5=
=½ (((a+b+c)(a+b-c)(a-b+c)(-a+b+c))^0,5/a)*
*(2bca^2/((b^2-c^2)(a+b+c)))/(bc(a+b+c)(b+c-a))^0,5=
=a(bc)^0,5((a+b-c)(a-b+c))^0,5/((b-c)(a+b+c)) (II)
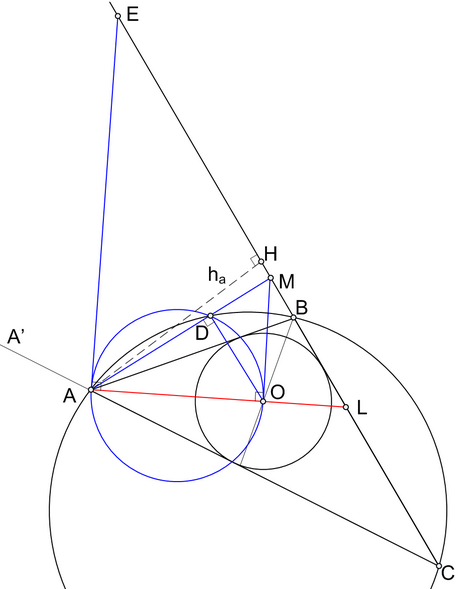
Сравнив (I) и (II), заметим, что OM^2=MB*MC, следовательно OM равен длине касательной, проведенной к описанной окружности треугольника ABC из точки M. Пусть точка D’ - второе пересечение секущей AM с описанной окружностью треугольника ABC. Построим на отрезке AO как на диаметре окружность W. Тогда точка D принадлежит этой окружности, поскольку ADO - прямой угол, а MO – касательная, проведенная к этой окружности из точки M. Поскольку касательные к окружности W и описанной окружности треугольника ABC, проведенные из точки M, равны,
MD*MA=MD’*MA=OM^2 и MD’=MD.
Следовательно, точки D И D’ совпадают и точка D лежит на описанной окружности треугольника ABC, ч.т.д.
P.S. Если кому удалось найти простое красивое решение, присылайте, с удовольствием опубликую!