 |
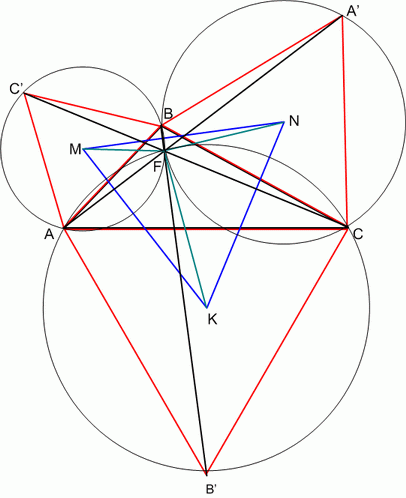
Построим треугольник ABC со сторонами 2,3,4. На его сторонах построим равносторонние треугольники ABC’, BCA’ и ACB’ вне треугольника ABC.
Проведем отрезки AA’, BB’, CC’ и обратим внимание на равенство треугольников ABA’ и CBC’ по двум сторонам и углу между ними и на тот факт, что они легко превращаются друг в друга поворотом на 60° вокруг точки B. Таким образом, угол между CC’ и AA’ равен 60°. Аналогично можно показать, что углы BFA’, A’FC, CFB’, B’FA также равны 60°. Тогда угол AFB равен 120° и опирается на AB со стороны, обратной углу AC’B, равному 60°, следовательно четырехугольник AC’BF вписанный. Соответственно, точка F лежит и на описанных окружностях треугольников ABC’, BCA’ и ACB’.
Соединив отрезками центры этих окружностей, получим треугольник MNK.
Поскольку FB – общая хорда окружностей с центрами M и N, она перпендикулярна отрезку MN, соединяющему их центры. Так же NK перпендикулярен FC, а MK перпендикулярен AF. Отсюда следует, что углы MNK, NKM и KNM равны 60°, т.е. треугольник MNK равносторонний.
Радиусы MF, NF, KF описанных окружностей треугольников ABC’, BCA’ и ACB’ пропорциональны соответственно 2, 3 и 4, следовательно, искомый треугольник может быть расположен относительно заданной точки P так же, как треугольник MNK относительно точки F.
Последний шаг: из точки P проводим отрезки PM’=2 параллельно FM, PN’=3 параллельно FN, PK’=4 параллельно FK.
Если же равносторонние треугольники на сторонах треугольника ABC построить обращенными во внутреннюю сторону треугольника ABC, треугольник MNK также окажется равносторонним, но меньших размеров, и даст второе решение, когда точка P находится вне искомого равностороннего треугольника.
Эти треугольники MNK называют большим и малым треугольниками Наполеона для треугольника ABC, утверждение об их равносторонности - теоремой Наполеона, а точку F - точкой Ферма треугольника ABC.
|
