
Примем за истину умалчиваемые аспекты условия: колодец имеет форму прямого круглого цилиндра, обе тростинки расположены в вертикальной плоскости, содержащей диаметр колодца. Изобразим на чертеже сечение колодца этой плоскостью. Итак, АВ=2, |СD|=3, |FG|=1, d=|AC| – искомый диаметр колодца. Обозначим через k отношение |CF|/|AF|. Рассматривая подобные треугольники, найдем:
|BC|=k+1, |AD|=(k+1)/k. Тогда
|AC|2 = 9 - ((k+1)/k)2 (1)
|AC|2 = 4 - (k+1)2 (2)
Вычитая (2) из (1), получим
((k+1)/k)2 - (k+1)2 = 5
или, после преобразований,
k4+2k3+5k2-2k-1=0
Говорят, можно попытаться решить «в лоб» уравнение четвертой степени и найти корень k=0,576128711, соответственно, диаметр колодца d=1,231185723 , но мы не станем торопиться, поскольку существуют сомнения в том, что древние египтяне умели решать уравнения четвертой степени, а наша задача состоит в поиске способа геометрического построения отрезка d, который потом легко измерить в долях имеющихся у нас, египтян, мер. Зафиксируем лишь, что
|AD|/|MD|=|CB|/|CN|=|CB|. (3)
Введем обозначения p=|AD|, q=|BC| и перепишем (1) и (2) в виде
d2=9-p2
d2=4-q2
Отсюда p2-q2=5. (4)
Кроме того, запишем (3) в виде q=p/(p-1) (3')
(p + q)*(p - q)=(50,5)2 (5)
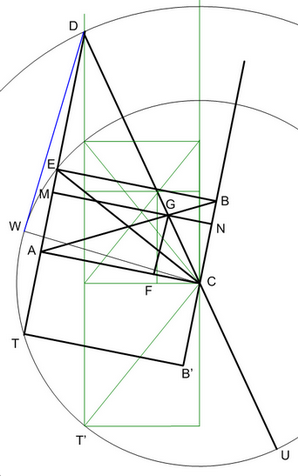
Построим две окружности радиусами 2 и 3 с центром в точке С. Из произвольной точки D окружности радиуса 3 проведем касательную DW к окружности радиуса 2. Легко установить, что длина касательной |DW|=50,5.
Через произвольную точку T на окружности радиуса 2 проведем из точки D секущую. Согласно теореме о касательной и секущей, наверняка известной египтянам, |DE|*|DT|=|DW|2
Опустим из центра окружностей перпендикуляр CA на хорду ET, проведем прямую CB || DT так, что EB || AC.
Заметим, что |AE|=|AT|=|BC|, |DE|=|AD|-|AE|=p-q и |DT|=|AD|+|AT|=p+q.
Поскольку |СD|=3, |AB|=2, наш рисунок представляет собой модель колодца Лотоса, где при любом положении точки Т на дуге WTU выполняется соотношение (5). Остается найти такое положение точки Т, при котором FG=1.
Вернемся к соотношению (3). Поскольку |MD|=|AD|-1, можно переписать уравнение (5) в виде:
(p + p/(p-1))*(p – p/(p-1))=5,
что равносильно
(p2-5)(p-1)2 – p2=0
или
(((p2-5)0,5)*(p-1) – p)*(((p2-5)0,5)*(p-1) + p) = 0
Рассмотрим первый сомножитель:
((p2-5)0,5)*(p-1) – p=0
(p2-5)0,5)= p/(p-1), (6)
Из выражения (6), с учетом (3) и (3'), следует, что существует прямоугольный треугольник с гипотенузой p и катетами 50,5 и q=p/(p-1).
Как же его построить?
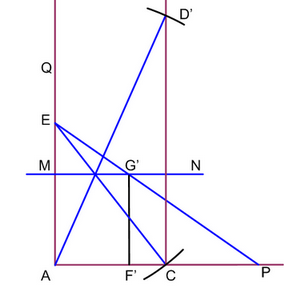
На высоте 1 над прямой AP параллельно ей проведем горизонталь MN. Отложим на линейке отрезок длиной 1 (на тростинке длиной 3 меры отложим отрезок длиной в 1 меру). Через точку P проведем прямую PЕ так, чтобы один из концов отложенного единичного отрезка линейки лежал на прямой AQ (точка Е), а другой - на прямой MN (точка G’). Тогда
|PE|/|PG’|=|AE|/|F’G’|=|AE|/|AM|=|AE|, т.е.
|PE|/(|PE|-1)=|AE|,
кроме того, |EP|2-|EM|2=|AP|2=5,
что соответствует выражениям (3’) и (6) для p и q.
Итак, |PE|=p=(k+1)/k, |AE|=q=k+1.
С центром в найденной точке Е раствором циркуля 2 сделаем засечку C на прямой AP.
Отрезок |АС| равен искомому диаметру d колода Лотоса. Проведем вертикаль через точку С и раствором циркуля 3 с центром в точке А сделаем на ней засечку D’.
Убедимся в том, что |СD’|=|PE|, и в том, что прямая AD’ (тростинка длиной 3) проходит через точку пересечения EC (тростинки длиной 2) и прямой MN (поверхности воды на высоте 1 над дном колодца).