 |
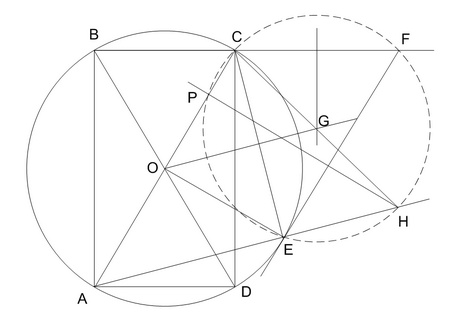
Строим срединный перпендикуляр к CF, затем через точку O перпендикуляр к СE. На их пересечении отмечаем центр G описанной окружности треугольника СEF. Проводим АЕ. Проводиm CG до пересечения с продолжением AE в точке H.
СН – диаметр описанной окружности треугольника СEF, поскольку СЕ перпендикулярно EH. Из H опускаем перпендикуляр на AC. Основание перпендикуляра P – искомая точка.
|
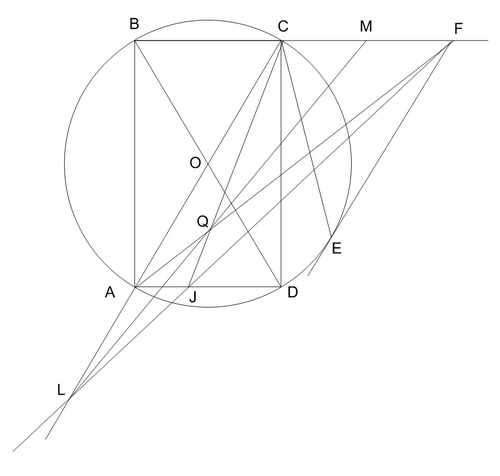 |
Пояснение 1. Известна теорема: прямая, проходящая через точку пересечения диагоналей трапеции и через точку пересечения ее непараллельных сторон, делит пополам каждую из параллельных сторон трапеции.
Можно было бы выбрать сразу трапецию ACFD, но в нашем примере AD почти || FD, поэтому возьмем на AD произвольную точку J и построим трапецию ACFJ. Найдем точку пересечения продолжений ее боковых сторон L и точку пересечения диагоналей Q. Проведем LQ до пересечения с CF в точке M, тогда M – середина CF.
|
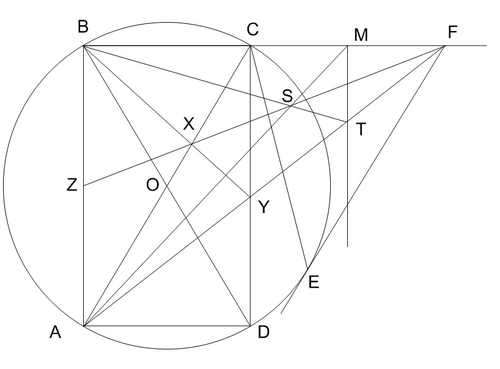 |
Пояснение 2. Для построения перпендикуляра к СF в точке M проведем через точку M прямую, параллельную CD. Для этого найдем сначала середину отрезка AB: проведем AF, отметим точку Y пересечения AF и CD. Проведем диагонали трапеции ABCY и отметим точку их пересечения X. Отметим точку Z пересечения FX и AB. Согласно упомянутой в Пояснении 1 теореме Z будет серединой AB. Теперь рассматриваем трапецию, одним основанием которой служит AB, а другое проходит через M, и нам нужно найти второй конец этого основания. Для этого проводим диагональ искомой трапеции AM и на ее пересечении с FZ отмечаем точку S. Вторую диагональ трапеции проводим через B и S и на пересечении BS и AF находим искомую вершину трапеции T.
Итак, MT перпендикулярен CF.
|
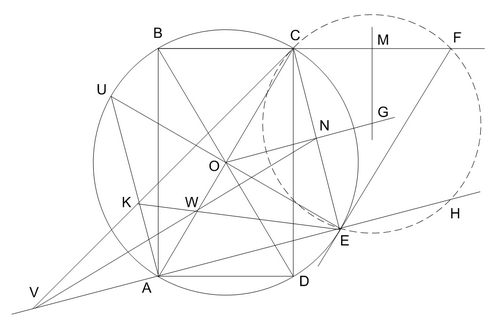 |
Пояснение 3. Пусть G - искомый центр описанной окружности треугольника ECF. Для построения срединного перпендикуляра к CE заметим предварительно, что CE является хордой данной окружности с центром O, следовательно, треугольник COE равнобедренный, и его высота ON будет искомым срединным перпендикуляром. Для поиска точки N Отметим второй конец U диаметра EO и соединим его с A. AU || CE. Выберем на AU произвольную точку K и, построив точку W пересечения диагоналей трапеции AKCE и точку пересечения ее боковых сторон V, на пересечении VW и CE найдем точку N. Проводим ON.
|
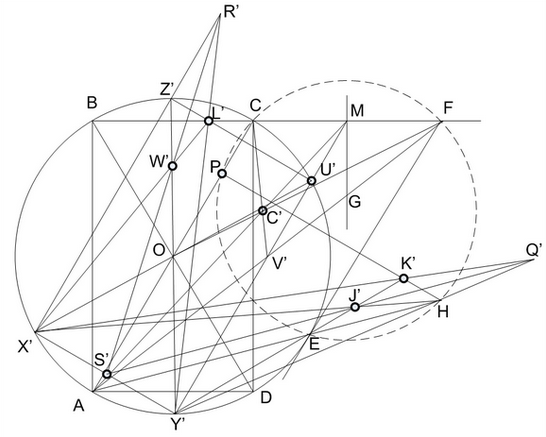 |
Пояснение 4. Для построения перпендикуляра к AC через точку H нам необходимо сначала построить хорду окружности, параллельную искомому перпендикуляру, а для этого нужно построить секущую окружности, отличную от диаметра, параллельную AC. Выберем отрезок AC в качестве основания трапеции с известной серединой в точке O. Пусть F будет пересечением продолжений ее сторон, а M - одной из вершин второго основания. Проведем AF, AM и OF. Точка C’ пересечения OF и AM является точкой пересечения диагоналей трапеции. Проводим CC’ до пересечения с AF в точке V’ - второй вершине основания MV’ трапеции ACMV’. Проводим секущую MV’ и отмечаем точки ее пересечения с окружностью U’ и Y’. Через O проводим диаметры U’X’ и Y’Z’. Тогда X’Y’ и U’Z’ параллельны искомому отрезку HP. Найдем точку S’ - середину X’Y’ с помощью трапеции X’Y’Z’L’, где L’ - произвольная точка на отрезке U’Z’. Проведем теперь Y’H и на его продолжении отметим произвольную точку Q’, которую используем как пересечение продолжений сторон трапеции с основанием X’Y’. Проведем X’Q’. Проведем S’Q’ и X’H и через точку их пересечения J’ проведем Y’J’. На пересечении Y’J’ и X’Q’ найдем вторую вершину K’ основания HK’ трапеции X’K’HY’. Наконец, проводим HK’ до пересечения с AC в искомой точке P.
|




