Решение задачи № 230

Пусть I – центр вписанной окружности остроугольного треугольника ABC, X и Y – точки касания окружности сторон AC и BC соответственно.
Через I проведена прямая g, пересекающая стороны AC, BC и окружность в точках K, L, M, N (в таком порядке слева направо).
P и Q – основания перпендикуляров, опущенных из точек X и Y на прямую g (точки P и Q находятся внутри окружности).
Доказать, что 1/KL+1/QM=1/MN+1/PL.

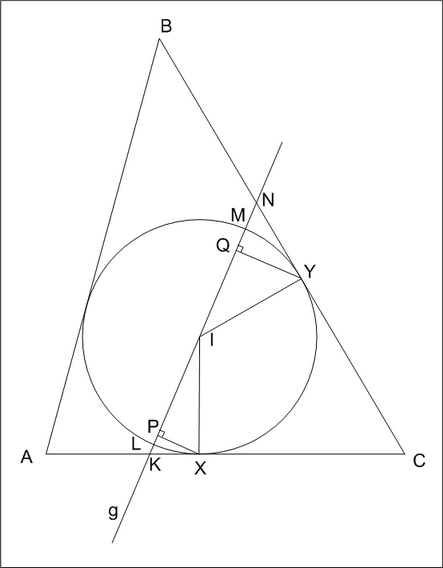
PL+PQ+QM=2r KL*KM=KX^2 MN*NL=NY^2 QY^2+QN^2=NY^2 PX^2+PK^2=KX^2 NY^2+r^2=IN^2 KX^2+r^2=KI^2 KI=KL+LP+PI=KL+r NI=NM+MQ+QI=MN+r PL*PM=PX^2 QM*QL=QY^2 QM*QL+(QM+MN)^2=MN*(MN+2r) QM*QL+QM^2+2QM*MN+MN^2=MN^2+2r*MN QM(QL+QM)+2QM*MN-2r*MN=0 QM*2r+2QM*MN-2r*MN=0 r(QM-MN)+QM*MN=0 r(MN-QM)=QM*MN PL*PM+(KL+PL)^2=KL*(KL+2r) PL*PM+KL^2+2KL*PL+PL^2=KL^2+2r*KL PL(PM+PL)+2KL*PL-2r*KL=0 PL*2r+2KL*PL-2r*KL=0 r(PL-KL)+KL*PL=0 r(KL-PL)=KL*PL (MN-QM)/(KL-PL)=QM*MN/ (KL*PL) (MN-QM)/(QM*MN)=(KL-PL)/ (KL*PL) 1/QM-1/MN=1/PL-1/KL 1/KL+1/QM=1/MN+1/PL чтд.

Назад На главную