
 |
Для начала попробуем представить, как выглядит описанная конструкция. Очень похоже, что общая часть двух кубов представляет собой 12-гранник, все грани треугольники - основания пирамид, отрезанных кубами друг от друга. Допустим, что мы обратно совместили оба куба, а затем начали поворачивать их вокруг главной диагонали в противоположные стороны синхронно. Тогда уходящие вправо части куба симметричны уходящим влево относительно неподвижной плоскости симметрии, проходящей через главную диагональ кубов. Таких плоскостей симетрии возникает 12, как видно на следующем рисунке (6 красных и 6 зеленых осевых линий на горизонтальной проекции). Вследствие этой симметрии при любом относительном угле поворота ребра кубов, не пересекающие главную диагональ, будут пересекать друг друга. Следовательно, можно считать доказанным, что общая часть двух кубов ограничена 12-ю равными треугольниками, общая площадь которых составит общую площадь поверхности фигуры, а общий объем двух кубов за вычетом объема 12-ти треугольных пирамид, отсекаемых кубами друг от друга, составит объем общей части кубов. Теперь можно перейти к вычислениям. |
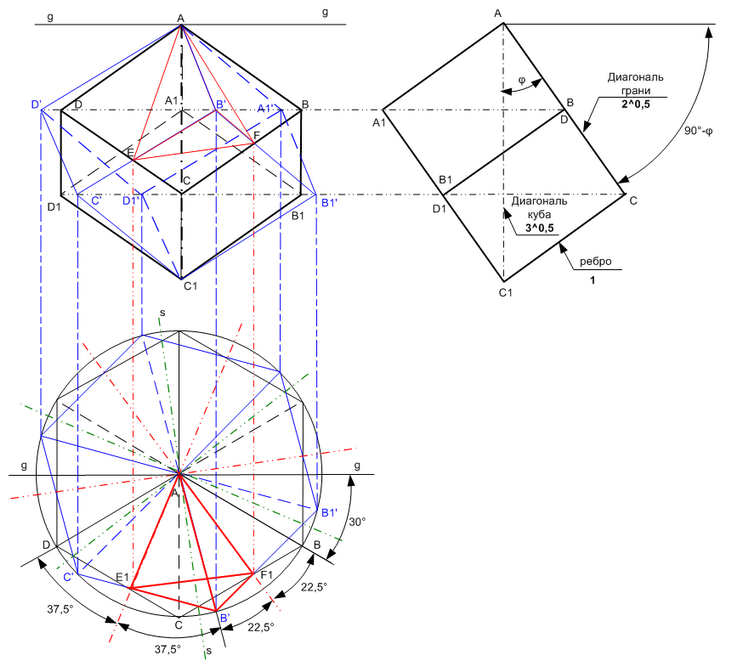 |
На виде сверху радиус описанной окружности, равный горизонтальной проекции ребра куба, составляет 1*cosφ
=(2/3)^0,5.
Пусть угол поворота куба β будет произвольным 0°<β<60°. В правильном треугольнике ACB угол AF1B=180°-60°-β/2=120°-β/2. Горизонтальную проекцию чевианы AF1 найдем по теореме синусов: sin60°/AF1=sin(120°-β/2)/AB AF1=AB*sin60°/(120°-β/2) Аналогично находим горизонтальную проекцию чевианы AE1 треугольника DAC: sin60°/AE1=sin(180°-60°-(60°-β/2))/AD AE1=AD*sin60°/sin(60°+β/2) Обратим внимание на то, что AB=AD, а sin(60°+β/2)= =sin(90°-30°+β/2)=sin(90°+30°-β/2)=sin(120°-β/2) Отсюда следует, что AE1=AF1= =((2/3)^0,5*sin60°/sin(60°+β/2) Это видно также в том, что треугольники E1F1C (черный куб) и E1F1B’ (синий куб) имеют общее основание и симметричны относительно прямой ss. Кроме того, в горизонтальной проекции угол E1AF1=120°-β/2-(60°-β/2)=60°, значит, треугольник E1AF1 равносторонний. Площадь треугольника AF1E1 равна: S1=½ AE1*AF1*sin60°= =½(AB1*sin60°/sin(60°+β/2))^2*sin60°= =½ * 2/3 * ¾ * 3^0,5/2 / (sin(60°+β/2))^2= =1/8*3^0,5/(sin(60°+β/2))^2 Истинная площадь треугольника AEF после поворота грани ABCD вокруг прямой gg на (90°-φ) до совпадения этой грани с горизонтальной плоскостью: Saef=S1/cos(90°-φ)=S1*3^0,5= =(3/8)/(sin(60°+β/2))^2 Соответственно, площадь поверхности фигуры, оказавшейся в пересечении кубов А и Б: S=12*Saef=(9/2)/(sin(60°+β/2))^2 Поскольку (sin(60°+β/2))^2 полого возрастает на участке 0°<β/2<30°, легко определить, что минимальная площадь общей части двух кубов будет наблюдаться при β/2=30°, т.е. при относительном повороте на 60°, и составит S=12*Saef= 9/2 = 4,5 а максимальная, соответственно, при β=0°: S=12*Saef=(9/2)/(sin(60°)^2=6 |
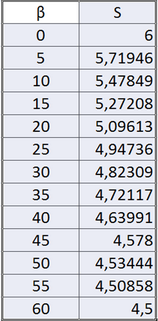 |
Составим таблицу искомой площади в зависимости от угла поворота β (с шагом 5°). Проверим «вручную» для угла β=45°: S=12*Saef=(9/2)/(sin(60°+β/2))^2=(9/2)/(sin82,5°)^2= =(9/2)/(1/8*(4+2^0,5*(1+3^0,5))) ≈ 4,578 Для справки: sin22,5°=((1-cos45°)/2)^0,5=(2-2^0,5)^0,5/2 cos22,5°=((1+cos45°)/2)^0,5=(2+2^0,5)^0,5/2 sin82,5°=sin(60°+22,5°)=sin60°cos22,5+sin22,5°cos6 0°= =3^0,5/2*(2+2^0,5)^0,5/2+(2-2^0,5)^0,5/2*½= =¼*(3^0,5*(2+2^0,5)^0,5+(2-2^0,5)^0,5) (sin82,5°)^2=1/16*(3*(2+2^0,5)+2*3^0,5*2^0,5+2-2^0,5)= =1/16*(6+3*2^0,5+2*3^0,5*2^0,5+2-2^0,5)= =1/16*(8+2*2^0,5+2*3^0,5*2^0,5)= =1/8*(4+2^0,5+3^0,5*2^0,5)= =1/8*(4+2^0,5*(1+3^0,5)) |