Допустим для простоты, что:
1) время t исчисляется в часах Ч;
2) равноденствие наступает в 12 часов по Ташкентскому времени 22 марта;
3) 22 марта является 81-м днем года;
4) количество часов в году =365,2564*24=8766,154; 8766,154;
5) высота башни h=375 м;
6) радиус Земли 6400 км;
7) координаты телебашни Ташкент φ=41° 19′ N, λ=69° 16′ E;
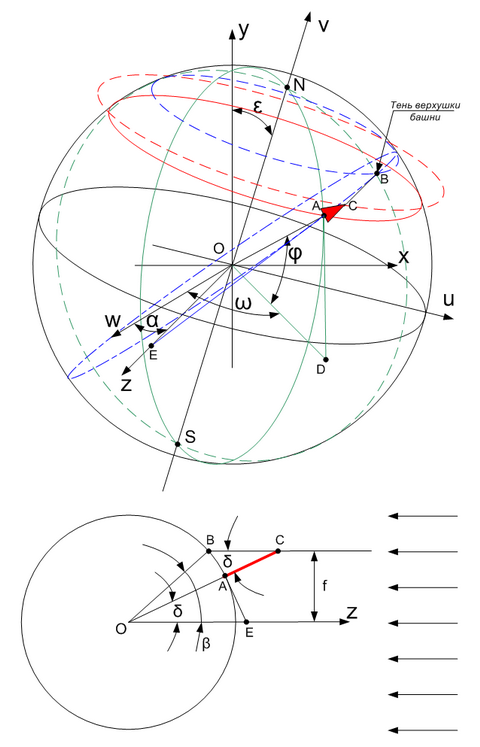
8) система координат Земли uvw, где ось w перпендикулярна оси вращения Земли, лежит в плоскости эклиптики и отклонена на угол α от радиус-вектора Земли на ее орбите в ее текущей точке, ось v, совпадающая с осью вращения Земли, отклонена от перпендикуляра к плоскости эклиптики на угол ε=23°26′;
9) система координат xyz связана с положением Земли на ее орбите, где ось x касается орбиты, ось y перпендикулярна плоскости эклиптики, ось z направлена к Солнцу;
10) все солнечные лучи, падающие на Землю, параллельны радиус-вектору Земли на её орбите в текущей точке;
11) в полдень 13 ноября Ч=7608.
Тогда от начала года до равноденствия пройдет 80*24+12=1932 часа, и текущий угол поворота радиус-вектора Земли от момента равноденствия составит:
α=2π*(Ч - 1932) / 8742,154
где Ч – порядковый номер текущего часа, считая с начала года.
Текущий угол поворота Земли вокруг своей оси запишем в виде:
ω=2π*(Ч - 1932)/23,93447
(Астрономические сутки взяты вместо земных для компенсации поворота земли вокруг своей оси за год за счет вращения вокруг солнца).
Рассмотрим декартовы координаты точки A - текущего положения основания башни в системе uvw:
u=r*cosφ*sinω
v=r*sinφ
w=r*cosφ*cosω
Определим те же координаты во вспомогательной системе u’yw, полученной поворотом системы uvw на угол ε вокруг оси w:
u'=u*cosε + v*sinε
y=v*cosε – u*sinε
u'= r*cosφ*sinω*cosε + r*sinφ*sinε
y= r*sinφ*cosε – r*cosφ*sinω*sinε
w=r*cosφ*cosω
Теперь определим координаты основания башни в системе xyz поворотом системы u’yw на угол α вокруг оси y:
z=w*cosα + u’*sinα
x=u’*cosα – w*sinα
x=r*(( cosφ*sinω*cosε + sinφ*sinε)*cosα - cosφ*cosω*sinα)
y= r*(sinφ*cosε – cosφ*sinω*sinε)
z=r*( cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα)
Найдем угол δ между радиус-вектором основания башни и направлением по оси z на Солнце:
cosδ=z/r
cosδ = cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα
Рассмотрим теперь сечение AOZ Земли, содержащее угол δ.
Вычислим расстояние c от основания башни до тени верхушки вдоль хорды Земной сферы:
f=(r+h)*sinδ
sinβ=f/r= (r+h)/r*sinδ
длина тени башни как ортодромии (дуги AB окружности большого диаметра Земли):
L=r*(β-δ)
Определим азимут тени башни как угол между касательной AD к меридиану башни в точке А и касательной АЕ к сфере Земли в точке А, лежащей в плоскости AOZ.
Координаты точки Е:
x=0
y=0
z=r/cosδ
Уравнение прямой AE:
(x-xA)/(xE-xA)= (y-yA)/(yE-yA)= (z-zA)/(zE-zA)
(x- r*(( cosφ*sinω*cosε + sinφ*sinε)*cosα - cosφ*cosω*sinα)/
(- r*(( cosφ*sinω*cosε + sinφ*sinε)*cosα - cosφ*cosω*sinα))=
=(y- r*(sinφ*cosε – cosφ*sinω*sinε))/(- r*(sinφ*cosε – cosφ*sinω*sinε))=
=(z- r*( cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα))/
( r/cosδ - r*( cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα))
Координаты точки D в системе uvw:
u=r/cosφ*sinω
v=0
w= r/cosφ*cosω
во вспомогательной системе u’yw поворотом системы uvw на угол ε вокруг оси w:
u'=u*cosε + v*sinε
y=v*cosε – u*sinε
u’= r/cosφ*sinω*cosε
y= - r/cosφ*sinω*sinε
w= r/cosφ*cosω
в системе xyz поворотом системы u’yw на угол α вокруг оси y:
z=w*cosα + u’*sinα
x=u’*cosα – w*sinα
x= r/cosφ*sinω*cosε*cosα - r/cosφ*cosω*sinα
y= - r/cosφ*sinω*sinε
z= r/cosφ*cosω*cosα + r/cosφ*sinω*cosε*sinα
Уравнение прямой AD:
(x-xA)/(xD-xA)= (y-yA)/(yD-yA)= (z-zA)/(zD-zA)
(x- r*(( cosφ*sinω*cosε + sinφ*sinε)*cosα - cosφ*cosω*sinα)/
((r/cosφ*sinω*cosε*cosα - r/cosφ*cosω*sinα) –
(r*(( cosφ*sinω*cosε + sinφ*sinε)*cosα - cosφ*cosω*sinα))=
=(y - r*(sinφ*cosε – cosφ*sinω*sinε))/
( - r/cosφ*sinω*sinε - r*(sinφ*cosε – cosφ*sinω*sinε))=
=(z - r*( cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα))/
((r/cosφ*cosω*cosα + r/cosφ*sinω*cosε*sinα) -
r*(cosφ*cosω + (cosφ*sinω*cosε + sinφ*sinε)*cosα))
Угол θ между прямыми AD и AE:
cosθ = |(xE-xA)*(xD-xA)+(yE-yA)*(yD-yA)+(zE-zA)*(zD-zA)| /
(((xE-xA)^2+(yE-yA)^2+(zE-zA^2))^0,5*((xD-xA)^2+(yD-yA)^2+(zD-zA^2))^0,5)
Теперь, глядя на башню сверху, мы можем построить траекторию тени ее верхушки в полярных координатах θ,L, где θ – азимут тени, L – длина тени.
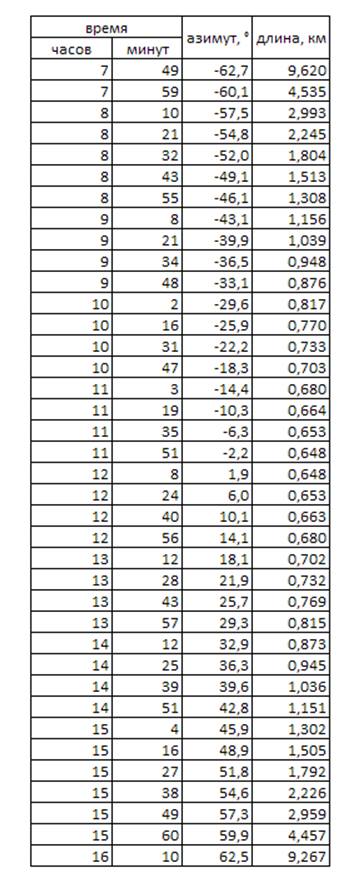
Расчеты по такой методике показывают путь тени верхушки башни на любую дату. Например, на 13 ноября.
Максимальная расчетная длина тени башни в любой день года составит 69,2 км. Когда солнце через несколько минут после восхода и за несколько минут до захода солнце находится под углом к горизонту 18' 36", т.е. когда луч солнца, проходящий через вершину башни, касается Земли.
Сомнительно, что кривую L(θ) можно привести к кривой 2-го или третьего порядка. Если принять постоянным наклон оси вращения Земли к плоскости ее орбиты в течение суток, а площадку, по которой проходит тень в течение дня, за плоскость, то кривая предстанет в виде участка эллипса. На самом же деле эллипс этот деформируется каждую секунду.
Необходимо отметить, что данное решение весьма приблизительно, не учитывает массу факторов, например, эллиптичность орбиты, волнообразность движения за счет вращения Земли вокруг центра масс системы Земля-Луна, произвольно выбранную фазу Земли в момент равноденствия, прецессию оси вращения Земли и т.д.
С другой стороны, размытие тени по мере удаления от основания башни, видимо, поглощает множество допущенных погрешностей.