Решение задачи № 31

С помощью циркуля и линейки восстановить треугольник по его описанной окружности и точкам (следам) M, B и H пересечения с ней продолжений медианы, биссектрисы и высоты, опущенных из одной вершины.

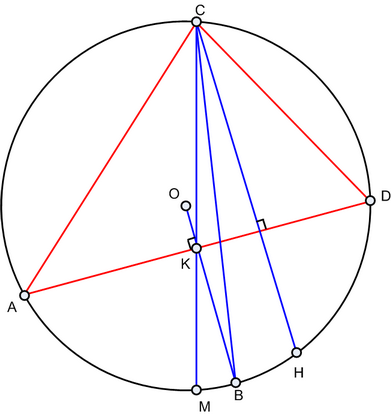
Пусть AD - основание искомого треугольника AD, C - вершина, из которой опущены высота, медиана и биссектриса. Поскольку биссектриса вписанного угла делит дугу, на которую опирается угол, на две равные части, отрезок BO будет перпендикулярен хорде AD. Параллельно OB проведем прямую через след высоты H, получив на пересечении с описанной окружностью вершину C искомого треугольника. Соединим ее со следом M медианы и через точку K пересечения OB и CM перпендикулярно OB проведем основание AD треугольника.

Назад На главную