Решение задачи №46

Имеются два одинаковых больших шара радиуса R, два одинаковых малых шара радиуса r, весьма длинный цилиндр радиуса p и плоскость. Всего шесть предметов. Как они расположены в пространстве – не сказано, но известно, что каждый из этих шести предметов касается остальных пяти, причем цилиндр касается плоскости по образующей, а шаров – боковой поверхностью. Зная радиус r малых шаров, найти радиусы R больших шаров и p цилиндра.

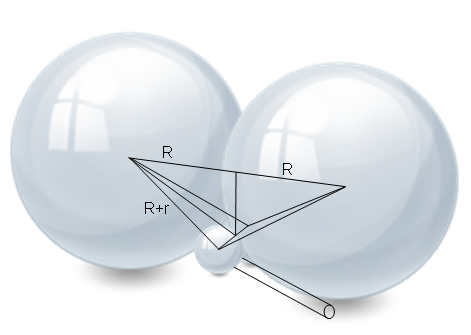
	Из первого рисунка (шары и цилиндр изобразим лежащими на горизонтальной плоскости) видим: (R+r)^2-r^2-(R-r)^2=R^2 (R+r+R-r)(R+r-R+r)-r^2=R^2 4Rr-r^2=R^2 R^2+r^2-4Rr=0 R=(4r+-(16r^2-4r^2)^0,5)/2 R=r(2+3^0,5)
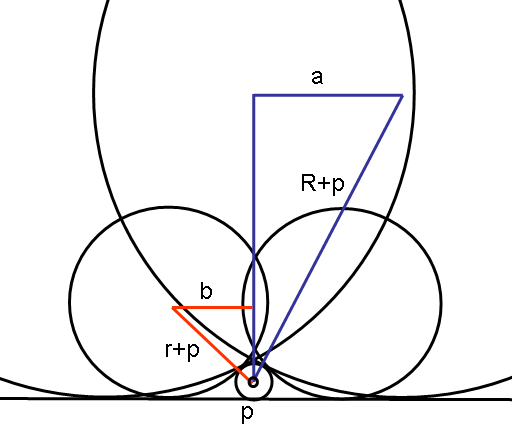
	На втором рисунке (плоскость рисунка перпендикулярна оси цилиндра) наблюдаем: a^2=(R+p)^2-(R-p)^2=4Rp b^2=(r+p)^2-(r-p)^2=4rp
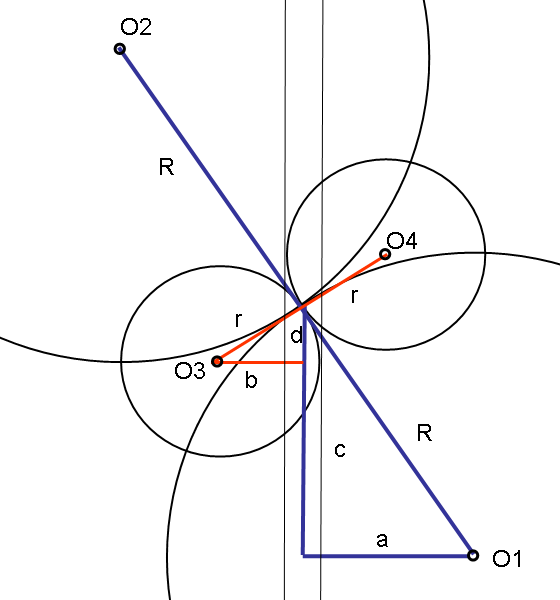
	на третьем рисунке (вид сверху на плоскость) из подобия синего и красного треугольников подмечаем: d/r=a/R. Далее без хитростей: d^2/r^2=a^2/R^2 d^2=r^2-b^2=r^2-4rp (r^2-4rp)/r^2=4Rp/R^2 p=rR/4(r+R) p=r^2(2+3^0,5)/4r(1+2+3^0,5) p=r(2+3^0,5)/4r(1+2+3^0,5) p=r(3+3^0,5)/24

Назад На главную