Решение задачи №4

Построить треугольник по стороне а, медиане m и радиусу R окружности, описанной около треугольника.

1. Медиана m опущена на сторону a. С центром в вершине C искомого треугольника проведем окружность радиусом описанной окружности R. С центром в точке O пересечения этой окружности с срединным перпендикуляром к стороне a проведем описанную окружность искомого треугольника. С центром в середине стороны a проведем окружность радиусом m. Точка пересечения ее с описанной окружностью и будет вершиной A искомого треугольника.

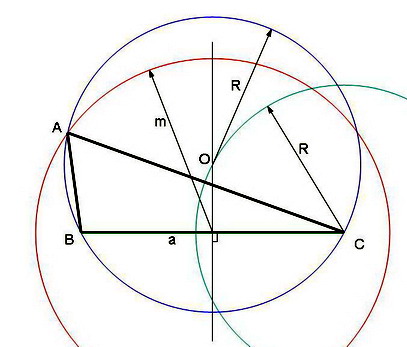
2. Медиана m опущена на сторону b треугольника. Описанную окружность строим аналогично п.1. С центром в вершине B построим окружность радиуса m. С центром в середине O' отрезка OC проведем окружность радиусом R/2. Получим описанную окружность треугольника, подобного искомому с коэффициентом подобия 1/2, с общей вершиной C, вершиной B' в середине a и вершиной A' в основании медианы m искомого треугольника, которая будет расположена на пересечении построенных окружностей радиусом m и R/2. Продолжив отрезок CA' до пересечения с описанной окружностью искомого треугольника, найдем его вершину A.

Назад На главную