 |
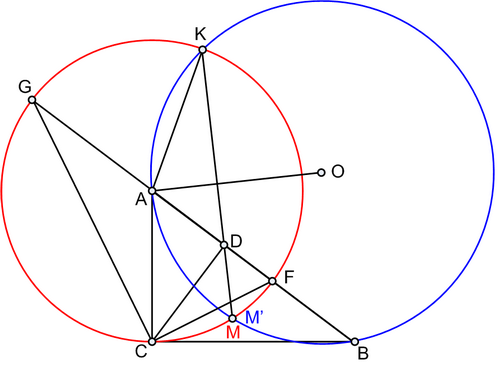
Продолжим AB до пересечения с окружностью А в точке G и KD до пересечения с окружностью А в точке М и окружностью О в точке М’. Поскольку CD – высота прямоугольного треугольника ABC, CD^2=AD*BD. Заметим, что AB и KM’ хорды окружности O, пересекающиеся в точке D, следовательно KD*DM’=AD*BD=CD^2. Отметим на гипотенузе АВ точку F пересечения с окружностью А. Проведем отрезок CG. GF – диаметр окружности, треугольник FGC прямоугольный и CD его высота. Следовательно, GD*DF=CD^2. Но GF и KM хорды окружности A, пересекающиеся в точке D, следовательно KD*DM=GD*DF=CD^2. Отрезки DM и DM’ лежат на одной прямой, имеют один общий конец в точке D и равны по величине DM=DM’=CD^2/KD. Следовательно точки M и M’ совпадают, т.е. KM является общей хордой окружностей A и O, соответственно, отрезок AO, соединяющий центры окружностей, перпендикулярен их общей хорде, что и требовалось доказать. |