Решение задачи №61

В описанной окружности равнобедренного треугольника ABC (с основанием AC) из вершины B проведена хорда BM. Из вершины C на прямую BM опущен перпендикуляр CH. Прямые AM и CH пересекаются в точке L. Найти геометрическое место точек L при движении точки М по окружности.

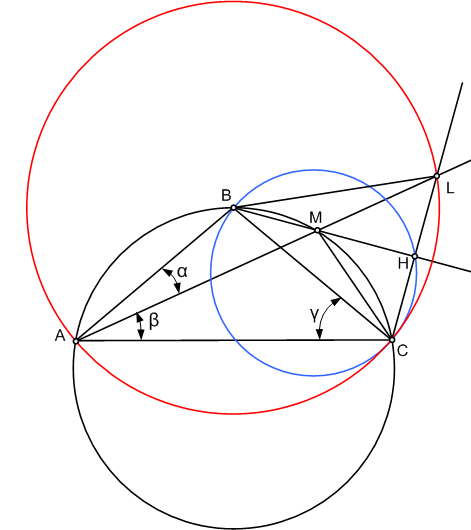
^HBC=β как опирающиеся на одну хорду МС. ^AMB=γ как опирающиеся на одну хорду AB. γ=α+β как углы при основании равнобедренного ΔABC. ^BCM=α как опирающиеся на одну хорду BM. ^MCH=90°- ^HMC =90° - (α + β) = 90°-γ ^LMH=^AMB как вертикальные углы, следовательно ^LMH=γ. ^MLH=90°-γ , следовательно ^MLH=^MCH, ΔMLH=ΔMCH, CH=HL, BL=BC. Таким образом, при движении точки M по описанной окружности треугольника АВС точка L движется по окружности с центром в вершине B треугольника и радиусом, равным боковой стороне треугольника.

Назад На главную