 |
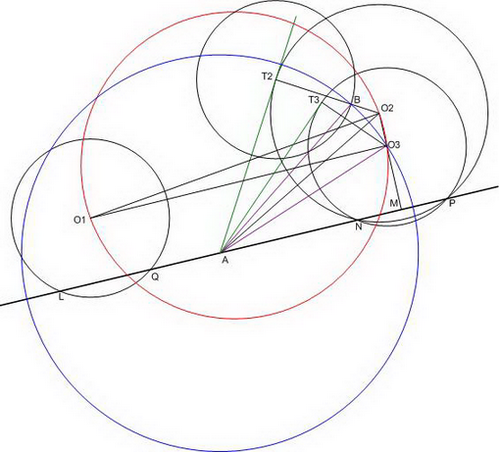
Пусть даны окружность радиуса r с центром в О1 и окружность радиуса R с центром в О2. Представим себе, что задача решена и прямая LP проведена через данную точку А так, что LQ=NP. Построим окружность О3 радиусом r так, что отсекаемая прямой LP хорда этой окружности совпадает с хордой NP окружности О2. Проведем касательные АТ2 и АТ3. Заметим, что секущая окружностей О2 и О3 делится на одинаковые отрезки АN и NP, следовательно АТ2=АТ3. На отрезке Т2О2 отложим r, получив точку В – центр окружности радиусом r с точкой касания Т2 прямой АТ2, совпадающей с точкой касания прямой АТ2 окружности О2. Заметим, что центры всех окружностей радиуса r, таких, что длина АТ2^2= APхNP, лежат на окружности с центром в А и радиусом АВ. С другой стороны, центр окружности О3 лежит на перпендикуляре O2M, опущенном на LP, и О2О3 перпендикулярно О1О3. Т.е. все искомые точки О3 – вершины прямого угла треугольника О1О2О3. Построив окружность на отрезке О1О2 как на диаметре, заметим, что искомая точка О3 лежат на этой окружности. Итак, О3 лежит на пересечении окружности с центром в А радиусом АВ и окружности, построенной на О1О2 как на диаметре. Существование точки пересечения этих окружностей и определяет решаемость данной задачи, в зависимости от расположения точки А. Если точка пересечения указанных окружностей существует, строим окружность радиусом r с центром в О3 и получаем точки N и Р, лежащие на искомой прямой. |