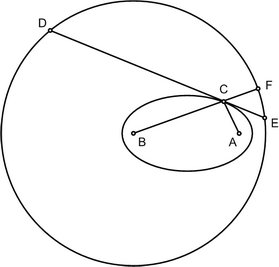
Выполним сначала некоторые построения, основанные на свойствах эллипса. Пусть дан эллипс с полуосями а и b. Отметим его фокусы А и B. С центром в фокусе B проведем окружность радиусом 2а. Через фокус В проведем в произвольном направлении прямую. Обозначим точку ее пересечения с эллипсом С, точку ее пересечения с окружностью F. Проведем отрезок СА и хорду окружности DE так, чтобы она касалась эллипса в точке С. Заметим, что углы DCB и FCE равны как накрест лежащие, DCB и ACE равны как углы между касательной и отрезками, соединяющими точку касания с фокусами эллипса, следовательно, углы FCE и ACE равны. Поскольку по определению эллипса |AC| + |BC| = 2a, |AC| = |CF|. Итак, треугольники ACE и FCE равны и симметричны относительно прямой DE. Точки А и F симметричны относительно прямой DE. Вернемся теперь к нашей задаче. Пусть на круглом листе бумаги отмечена произвольная точка А. Согнем лист, совместив точку А с произвольной точкой окружности листа. Зафиксируем линию сгиба, чтобы при разгибании листа на бумаге остался след в виде хорды окружности. Последовательно совмещая точку А с разными точками на окружности и фиксируя линии сгиба, получим семейство хорд, касательных к эллипсу, фокусами которого являются точка А и центр круга. Чем больше сгибов, тем отчетливее виден огибающий семейство касательных эллипс.