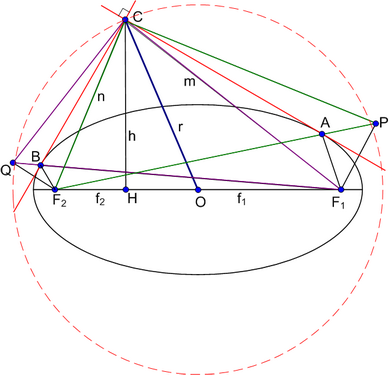
в точках А и В.
Отметим точку P, симметричную фокусу F1 относительно прямой AC,
и точку Q, симметричную фокусу F2 относительно прямой BC.
Обозначим через m отрезок |F1С|=|PC|, через n отрезок |F2С|=|QC|.
Поскольку касательная к эллипсу в точке А является биссектрисой угла
между продолжением прямой F2A и АF1, точки F2, A и P лежат на одной прямой и |F2P|=2a, аналогично |F1Q|=2a. Треугольники QCF1 и PCF2 равны по трем сторонам и являются прямоугольными.
Следовательно, |F1P|2=|F2Q|2=n2+m2=4a2.
Проведем высоту |СH|=h треугольника F1CF2, обозначим f1=|F1H|, f2=|F2H|.
m2-h2+n2-h2=f12+f22 ; m2+n2=2h2+f12+f22 (I)
r2=h2+(c-f1)2=h2+c2-2cf1+f12
r2=h2+(f2-c) 2=h2+c2-2cf22+f22
2r2=2h2+2c2-2c(f1+f2)+f12+f22=2h2-2c2+f12+f22 (II)
Вычитая (I) из (II), имеем:
2r2-m2-n2=-2c2 , т.е. r2=(1/2)(m2+n2)-c2 (III)
Подставив в (III) n2+m2=4a2 и с2=a2-b2, получим:
r2=a2+b2
при любом положении прямого угла ACB, касающегося эллипса обеими сторонами.