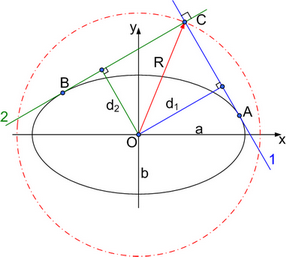
Запишем уравнение эллипса с полуосями а и b в виде x = a cos t; y = b sin t.
Найдем уравнение касательной 1 к эллипсу, приняв, что параметр t соответствует точке А эллипса:
y=(-b/a)ctgt x + (b/a) ctgt a cost + b sint
перепишем его в виде
b cost x + a sint y – ab = 0
тогда квадрат расстояния d1 от центра эллипса до прямой 1 определится как
d12 = a2b2 / (b2cos2t + a2sin2t)
Примем для точки В x = a cos t1; y = b sin t1. С учетом перпендикулярности касательных 1 и 2 заметим, что
k2 = - 1/k1 , т.е. ctgt1 = - (a2/(b2ctgt)) ,
соответственно sint1 = 1/(1+(a4/b4)tgt)1/2 ;
cost1 = - (a2/b2)tgt/(1+(a4/b4)tgt)1/2 .
Запишем уравнение касательной в точке В:
y=(-b/a)ctgt1 x + (b/a) ctgt1 a cost1 + b sint1
Выразим функции от t1 через функции от t:
y=(-b/a)(-a2/b2)tgt x +(b/a)(-a2/b2)tgt a(-a2/b2)tgt/(1+(a4/b4)tgt)1/2+b/(1+(a4/b4)tgt)1/2;
после упрощений приведем уравнение касательной в точке В к виду:
a sint (b4cos2t+a4sin2t)1/2 x + b cost (b4cos2t+a4sin2t)1/2 y + a4sin2t + b4cos2t = 0.
Найдем квадрат расстояния d2 от центра эллипса до прямой 2:
d22 = (a4sin2t + b4cos2t) / (b2cos2t + a2sin2t) .
Вычислим квадрат расстояния R от центра эллипса О до вершины С прямого угла:
R2 = d12 + d22 = a2b2/(b2cos2t + a2sin2t) + (a4sin2t + b4cos2t)/(b2cos2t + a2sin2t) .
После преобразований получаем R2 = a2 + b2.
Итак, R не зависит от t и вершина C прямого угла при обкатывании вокруг эллипса перемещается по окружности радиусом
R=(a2+b2)1/2 .