Задача № 63. Заливное.
Четверг, июля 16, 2009Лаборант Михалыч вынул пробку, и тут ему позвонили. На столе образовалась лужа глубиной около 1. Оцените форму лужи.
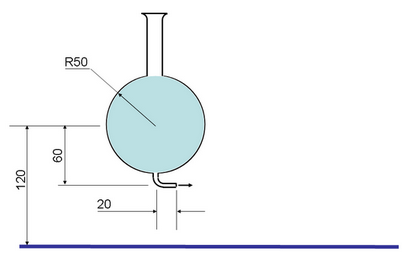
Из объяснительной Михалыча впоследствии выяснилось, что пробка была диаметром 5.
Лаборант Михалыч вынул пробку, и тут ему позвонили. На столе образовалась лужа глубиной около 1. Оцените форму лужи.

Из объяснительной Михалыча впоследствии выяснилось, что пробка была диаметром 5.
Шарик для настольного тенниса (m=2,7 г, R=20 мм) заполнен наполовину растительным маслом (плотностью p=0,9 г/см^3) и опущен в пустой цилиндрический стакан радиуса 25 мм. Сколько воды нужно налить в стакан, чтобы шарик перестал опираться на дно стакана?
Для любителей начертательной геометрии.
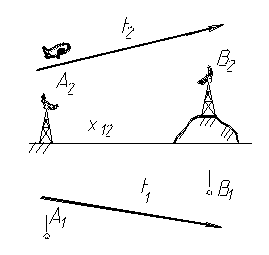
В точках А и В находятся радиолокаторы. Самолет перемещается в направлении t. Определить точки, в которых лучи локаторов будут сходиться к самолету, пересекаясь под прямым углом.
Имеются два одинаковых больших шара радиуса R, два одинаковых малых шара радиуса r, весьма длинный цилиндр радиуса p и плоскость. Всего шесть предметов. Как они расположены в пространстве – не сказано, но известно, что каждый из этих шести предметов касается остальных пяти, причем цилиндр касается плоскости по образующей, а шаров – боковой поверхностью. Зная радиус r малых шаров, найти радиусы R больших шаров и p цилиндра.
Б. Делоне, О. Житомирский
В шаровой сегмент вписан шар, касающийся сферы сегмента в точке А и плоскости сегмента в точке В. Другой вписанный в тот же сегмент шар касается сферы сегмента в точке А’ и плоскости сегмента в точке В’. Доказать, что для любых шаров, вписанных в данный сегмент, прямые AB и A’B’ пересекаются в общей точке С, лежащей на сфере.
Клоуны в перерыве между номерами играли за кулисами на бильярде. В пылу азарта один из них так ударил по шару, что шар вылетел со стола и, пробив бумажный колпак напарника, запрыгнул в горшок с пальмой, где и потерялся навеки. Расследуя обстоятельства пропажи шара, администратор цирка решил лично провести баллистическую экспертизу. Выполнив развертку пришедшего, заметьте, в негодность коническго колпака, администратор был весьма удивлен формой отверстий. И даже, что не характерно для администраторов, составил уравнение контура каждого отверстия. А вы можете повторить его подвиг?
Определите площадь треугольника ММК: Мадрид-Москва-Калькутта.
С помощью циркуля и линейки построить на плоскости радиус данного шара.
Известна теорема Мансиона:
Отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
Рискнем распространить ее на пространственные формы:
Отрезок, соединяющий центры вписанной и вневписанной сфер тетраэдра, делится описанной сферой пополам.
Докажите или опровергните.
Через произвольную точку внутри сферы проведены три взаимно перпендикулярные хорды, разбитые данной точкой на отрезки a и b, c и d, e и f соответственно. Найти радиус сферы.
Старинная задача от Мартина Гарднера
Через центр шара просверлено сквозное круглое отверстие длиной 6 см. Найти объем оставшейся части шара.
Основанием наклонной пирамиды является неправильный пятиугольник ABCDE. На основании, касаясь его в точке P лежит шар радиуса R, касающийся всех боковых рёбер пирамиды. Снизу в точке Q основания касается второй шар радиуса 2R, касается он и продолжений всех боковых рёбер пирамиды. Расстояние между центрами шаров равно 4R. Найти сумму расстояний |PC| и |QC|.
На горизонтальной плоскости стоит вертикально тонкое кольцо радиуса R. Масса кольца M. С внутренней стороны кольцо имеет канавку, по которой может кататься без трения шарик радиуса r массой m. Шарик располагают в канавке в правой полюсной точке кольца и отпускают. Коэффициент трения качения кольца по плоскости равен k. Как далеко и в какую сторону укатится кольцо? По какой траектории будет двигаться шарик в неподвижной системе координат?
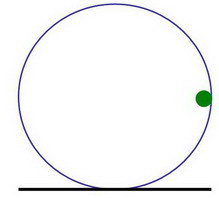
Хорошо забытое старое
Три шара разных диаметров лежат на плоскости, касаясь друг друга. Сверху их касется другая плоскость. Найти угол между плоскостями.