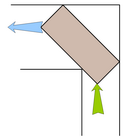
Петя Васильчиков — гениальный ребенок. Так полагает его бабушка Элеонора Бельц. Разумеется, каждый гениальный ребенок просто обязан стать гениальным пианистом. «Только Ronisch 132 !» – настаивала бабушка под самый Новый год. И вот, грузчики Михалыч и Пахомыч пытаются мимо наряженной ёлки закатить пианино в Петину комнату. Для этого им необходимо преодолеть поворот коридора. Ширина коридора до поворота 130 см, длина пианино 152 см, ширина 63 см. Известно, что слегка зацепив обои, но не поцарапав при этом инструмент, грузчики справились с задачей. Какова же была ширина коридора после поворота? Да, интересно также, какой формы следы оставили на полу колеса пианино весом 235 кг.
фольклор
