Вершина прямого кругового конуса расположена в вершине A куба ABCDA’B’C’D’, а основанием является окружность, построенная на диагонали BA’ грани ABB’A’ куба. Вершина второго прямого кругового конуса также совпадает с вершиной A куба, а основанием является окружность, построенная на диагонали A’D грани ADD’A’ куба. Найти отношение объема общей части конусов к объему куба.
В кружке диаметром d поверх кофе не смешивающийся с ним слой сливок. На сколько градусов нужно наклонить кружку, чтобы слой сливок стал вдвое тоньше? Какой уровень кофе в кружке должен был быть первоначально, чтобы при требуемом наклоне не обнажилось дно? Какой высоты должна быть кружка, чтобы при требуемом наклоне ни капли сливок не пролилось?
Парабола задана на плоскости фокусом и директрисой. На той же плоскости отмечены произвольно точки P и Q. С помощью циркуля и линейки найти точки пересечения параболы и прямой.
«Увидел Садко: во синем море
Стоит палата белокаменная.»
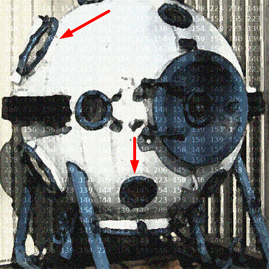
Лампа внутреннего освещения в батисфере диаметром D расположена в её верхней полюсной точке. В боковой поверхности верхней полусферы имеется круглый иллюминатор диаметром d1, а в боковой поверхности нижней полусферы — диаметром d2. Ось верхнего иллюминатора наклонена под 45° к горизонту, а нижнего — под 60°. Батисфера встала на горизонтальном участке дна на шасси так, что нижняя полюсная точка сферы оказалась на высоте h над дном. Какую форму и размеры будут иметь световые пятна на дне от лучей, проходящих через иллюминаторы?
Толщиной стенок, преломлением, рефракцией и рассеянием света Садко пренебрег, ну и мы тоже.
Цилиндрический ролик длиной L и диаметром D катится по горизонтальной плоскости без проскальзываний. В некоторый момент времени диаметр одного из оснований цилиндра начинает меняться пропорционально углу поворота ролика вокруг своей оси (при этом прямолинейность образующей сохраняется, т.е. ролик становится усеченным конусом) и уменьшается за два оборота ролика вокруг своей оси от D до нуля. Какую траекторию опишет на плоскости точка касания малого основания ролика к плоскости?
Во внутренней полости конуса с вертикальной осью и углом при вершине A на высоте H от вершины конуса вдоль его внутренней поверхности под углом к горизонтали B запускают шарик радиуса r с начальной скоростью v. Трение между конусом и шариком отсутствует, поверхности конуса и шарика абсолютно тверды. Какова будет траектория шарика?
Е.Скляревский
Дорогая редакция!
Пишет вам Петя Пробиркин из секретной химической лаборатории Спецсредмашпоставки города N-ска. В нашей лаборатории я служу программистом робототехники. Роботы наши в герметически закрытом помещении переливают и смешивают ядовитые реактивы. Сосуды используются при этом старинные: чашки Петри, колбы, стаканы, пробирки, мензурки, реторты и т.д. Сосуды цилиндрические, конические, полусферические, сферические. Передо мной поставили задачу запрограммировать роботов определенным образом. Для каждой пары изливающего и приемного сосудов разной формы робот должен выбирать такой закон изменения угла наклона изливающего сосуда от времени, чтобы уровень жидкости в приемном сосуде рос с постоянной скоростью. Вязкостью и поверхностным натяжением разрешили пренебречь. Помогите, люди добрые, алгоритмами!
Имеется тонкостенная коническая колба диаметром у основания 100 мм, углом при вершине конуса 90 градусов, с цилиндрическим горлышком диаметром 20 мм. В колбу пропихнули эластичный резиновый шарик диаметром 50 мм и плотностью 0,5 г/см^3. Колбу затем наполнили водой и опрокинули. Сколько воды останется в колбе, если при касании шариком стенки колбы или её горлышка, он запирает собой отверстие?
Вавилонская башня. По боковой поверхности конуса винтовая лестница. При постоянном шаге винта угол подъема лестницы по мере приближения к верхушке башни увеличивается. А можно ли построить сужающуюся кверху башню такой формы, чтобы и шаг винта лестницы был постоянным, и угол её подъема сохранялся одинаковым от подножья до верхушки?
Вот среди ночи тайком взяли Вы, к примеру, конус из детского набора деревянных фигур и из баловства, ну вот буквально от нечего делать, не задумываясь, начертили у него на боку циркулем «окружность». Ну и конечно же заметили, что окружность какая-то не круглая. И на развертке конуса не круглая. И вообще никак не круглая. И решили составить уравнение этой кривулины на развертке конуса. Вот и мучайтесь! Да. А я спать пошел. 🙂
Венчать новогоднюю ёлку в институте геодезии и картографии должен будет глазастый глобус размером с голову с нарисованной улыбкой в районе Фолклендских островов. Инженеры-картографы, закончив крепить резинки-венгерки на новогодние же карнавальные колпаки, шутки ради надели на глобус четыре колпака, и оказалось, что каждый из колпаков касается трех других на поверхности глобуса. Вот интересно, на какую параллель опирается колпак, надетый на северную макушку глобуса? И каково расстояние между верхушками колпаков, если длина экватора глобуса 56 см, а высота колпаков 40 см?
Дружные осьминоги соорудили стелу в память о Первом Великом Всплытии. Стела в виде конуса высотой 3 м, диаметром у основания 1 м. Памятная надпись, как положено у осьминогов, должна пройти по спирали от вершины к основанию конуса. Шрифт дружные осьминоги выбрали высотой 10 см, с константной шириной знака в 8 см, межстрочным интервалом 2 см. Надпись гласила: «Слава нашим Первым Доблестным Всплывателям, впервые увидевшим Солнце как оно есть и поведавшим об этом миру, что позволило вывести новые сорта осьминожьего тюльпана и лечить прежде неизлечимую осьминожью скрутку солнечными ваннами! Год 59574309 от сотворения Моря.»
И задумались, а уместится ли надпись? Помогите дружным осьминогам!
Начертим на бумаге сектор круга. Соединим хордой концы дуги сектора. Свернём сектор в конус, совместив его крайние радиусы. В какую кривую превратится хорда? Будет ли она плоской кривой? Как записать ее уравнение?
Клоуны в перерыве между номерами играли за кулисами на бильярде. В пылу азарта один из них так ударил по шару, что шар вылетел со стола и, пробив бумажный колпак напарника, запрыгнул в горшок с пальмой, где и потерялся навеки. Расследуя обстоятельства пропажи шара, администратор цирка решил лично провести баллистическую экспертизу. Выполнив развертку пришедшего, заметьте, в негодность коническго колпака, администратор был весьма удивлен формой отверстий. И даже, что не характерно для администраторов, составил уравнение контура каждого отверстия. А вы можете повторить его подвиг?
Основанием наклонной пирамиды является неправильный пятиугольник ABCDE. На основании, касаясь его в точке P лежит шар радиуса R, касающийся всех боковых рёбер пирамиды. Снизу в точке Q основания касается второй шар радиуса 2R, касается он и продолжений всех боковых рёбер пирамиды. Расстояние между центрами шаров равно 4R. Найти сумму расстояний |PC| и |QC|.
