Архив на месяц ноября, 2010
Воскресенье, ноября 28, 2010
Из центра O окружности опущен перпендикуляр OA на прямую l. На прямой l взяты точки B и C так, что AB = AC. Через точки B и C проведены две секущие, первая из которых пересекает окружность в точках P и Q, а вторая — в точках M и N. Прямые PM и QN пересекают прямую l в точках R и S. Докажите, что AR = AS.
ЦРДО им. Бернулли
Категория: задачи на доказательство | 2 Комментариев »
Суббота, ноября 27, 2010
Имеется обод велосипедного колеса диаметром d, способный стоять или катиться по горизонтальной плоскости, оставаясь в вертикальной плоскости. Вдоль хорды AB обода натянута струна длиной t. На струне в точках P и Q укреплены шары массами M и m соответственно. |AP|=a, |PQ|=b. Найти точки обода, стоя на которых он будет находиться в равновесии. В какой из них равновесие будет устойчивым?
Категория: Задачи на вычисление, Механические утехи, около физики, Подумалось вдруг, этюды | Нет комментариев »
Четверг, ноября 25, 2010
Каким минимальным числом полос изоленты шириной 1 см можно обклеить куб с ребром N см, использовав при этом минимальное количество изоленты, если ленты можно клеить только параллельно ребрам куба?
Е. Скляревский. По следам problems.ru
Категория: Задачи на вычисление, Куб, площадь | 4 Комментариев »
Четверг, ноября 25, 2010
На диаметре AB окружности выбрана произвольно точка D. Перпендикуляр к AB, проведенный через точку D, пересекает окружность в точке C. На AD и DB как на диаметрах построены окружности. Общая касательная к этим окружностям, пересекающая CD, касается их в точках M и N соответственно. Доказать, что отрезок AC проходит через точку M, а BC — через N.
Николай Москвитин
Категория: задачи на доказательство, треугольник | Нет комментариев »
Четверг, ноября 18, 2010
Доказать: сумма квадратов расстояний от некоторой точки окружности одного основания цилиндра до концов некоторого диаметра окружности противоположного основания (высота цилиндра и радиус основания считаются постоянными) не зависит ни от выбора точки, ни от выбора диаметра.
Николай Москвитин
Категория: задачи на доказательство, этюды | Нет комментариев »
Четверг, ноября 11, 2010
В прямоугольном треугольнике ABC с прямым углом B проведены биссектриса AD, высота BE. Биссектриса BF угла ABE и биссектриса BG угла EBC пересекают биссектрису AD в точках J и I соответственно.
Доказать: ΙΒ=IJ=IG=IE.
Николай Москвитин
Категория: задачи на доказательство, треугольник | Нет комментариев »
Четверг, ноября 11, 2010
В квадрате ABCD отмечены середины Е и F двух соседних сторон BC и CD соответственно и проведены прямые AE и BF, пересекающиеся в точке G. Около квадрата описана окружность. Точка пересечения прямой AE с нею- точка H. Доказать: GE=EH.
Николай Москвитин
Категория: задачи на доказательство, квадрат, четырехугольник | Нет комментариев »
Четверг, ноября 11, 2010
Дано: треугольник ABC. Известно, что высота BD образует со стороной BC угол в 45 градусов. Считается, что прямая BD, содержащая высоту, уже построена. Как всего одним движением циркуля построить ортоцентр треугольника ABC?
Николай Москвитин
Категория: Задачи на построение, треугольник | Нет комментариев »
Четверг, ноября 11, 2010
Дана равнобедренная трапеция. Доказать следующие утверждения:
1)Точки пересечения прямых, проходящих через вершины тупых углов трапеции и образующих (попарно) равные углы одна с верхним основанием, другая с боковой стороной трапеции, и вершины тупых углов лежат на одной окружности.
2)Центр этой окружности лежит на пересечении перпендикуляров к боковым сторонам трапеции, проходящих через эти вершины, причём угол, образуемый этими прямыми, в два раза больше осторого угла трапеции. (аналогичные утверждения можно вывести для другого основания с той оговоркой, что во втором утверждении указанный угол будет больше 180 градусов.)
Николай Москвитин
Категория: задачи на доказательство, Классика, четырехугольник | Нет комментариев »
Вторник, ноября 9, 2010
Радиус купола R, коэффициент трения лапок птиц о купол k. Сколько птиц поместится на куполе, если одна птица занимает площадь S? Еще надо уточнить, что птички — неделимые, недеформируемые кружки площадью S.

Е.С. Скляревский Компот
Категория: Задачи на вычисление, Механические утехи, около физики, площадь, этюды | Нет комментариев »
Вторник, ноября 9, 2010
Мячик скатывается под действием силы тяжести по обрезанному параболическому трамплину y(x)=(x-a)^2+b — находясь в начальный момент в точке x=0 y=a^2+b, a и b>0 — определить в какой точке обрезать параболу, чтоб дальность полета была максимальной.
YuK
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, около физики, Парабола | Нет комментариев »
Четверг, ноября 4, 2010
Двухметровая доска лежит на асфальте одним концом, середина доски опирается на трубу. На конце доски буртик, в который упираются уложенные в продольный желобок доски в ряд десять теннисных мячей. Угол наклона доски в первоначальном состоянии 20 градусов к горизонту. На второй конец доски с высоты 1 метр бросают пудовую гирю. На каком расстоянии друг от друга приземлятся мячи?
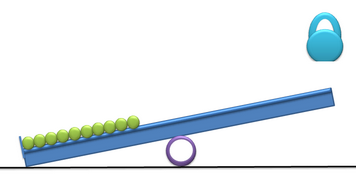
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, около физики, Парабола, Подумалось вдруг, шары, этюды | 5 Комментариев »
Четверг, ноября 4, 2010
Имеется тонкостенная коническая колба диаметром у основания 100 мм, углом при вершине конуса 90 градусов, с цилиндрическим горлышком диаметром 20 мм. В колбу пропихнули эластичный резиновый шарик диаметром 50 мм и плотностью 0,5 г/см^3. Колбу затем наполнили водой и опрокинули. Сколько воды останется в колбе, если при касании шариком стенки колбы или её горлышка, он запирает собой отверстие?
Категория: Задачи на вычисление, конус, Механические утехи, Объём, около физики, Подумалось вдруг, шары, этюды | Нет комментариев »

