Задачи по геометрии

Парабола задана на плоскости фокусом и директрисой. На той же плоскости отмечены произвольно точки P и Q. С помощью циркуля и линейки найти точки пересечения параболы и прямой.

В окружности проведена хорда AB, меньшая диаметра, в полученные сегменты вписаны окружности. I-центр меньшей из них. Известно, что прямая AI и касательная из точки A к большей окружности перпендикулярны.
Найти отношение радиусов.

_{Николай Москвитин}

Уважаемые посетители, сайту geom.uz исполнилось 4 года. Есть повод подвести итоги. Буду рад услышать ваши отклики, предложения, замечания. Пишите сюда в комментарии или на geomuz[at]yandex.ru ! Присылайте оригинальные задачи!
🙂

На горизонтальной прямой установлены в вертикальной плоскости, содержащей данную прямую, три окружности радиусов R1, R2 и R3, имеющие общую точку касания между собой и с прямой. Данную точку помечают на прямой как A, на окружностях соответственно A1, A2 и A3. В некоторый момент времени все три окружности начинают катиться по прямой без скольжения в одну сторону с одинаковой для всех трех окружностей и постоянной угловой скоростью w. Доказать, что при этом в любой момент времени точки A, A1, A2 и A3 находятся на одной прямой. Найти зависимость наклона этой прямой к горизонту от времени.

Две противолежащие стороны четырёхугольника равны и суммы квадратов его противолежащих сторон также равны.
Доказать, что две равных стороны этого четырёхугольника будут видны под прямым углом из точки, равноудалённой от концов одной диагонали на одно расстояние и от концов другой — на другое.

_{Николай Москвитин}

Вокруг треугольника ABC описана окружность, и в ней проведён диаметр AD; в треугольнике проведена высота BE, из B проведён перпендикуляр BF на AD.
Доказать: отрезок EF проходит через середину стороны BC.

_{Николай Москвитин}

«Увидел Садко: во синем море
Стоит палата белокаменная.»

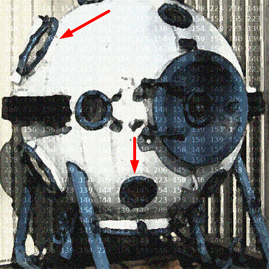
Лампа внутреннего освещения в батисфере диаметром D расположена в её верхней полюсной точке. В боковой поверхности верхней полусферы имеется круглый иллюминатор диаметром d1, а в боковой поверхности нижней полусферы — диаметром d2. Ось верхнего иллюминатора наклонена под 45° к горизонту, а нижнего — под 60°. Батисфера встала на горизонтальном участке дна на шасси так, что нижняя полюсная точка сферы оказалась на высоте h над дном. Какую форму и размеры будут иметь световые пятна на дне от лучей, проходящих через иллюминаторы?
Толщиной стенок, преломлением, рефракцией и рассеянием света Садко пренебрег, ну и мы тоже.

Добрые инопланетяне, прибывшие к нам на орбиту с дружественным визитом, для установления контакта любезно умыкнули Вас к себе на корабль, тепленьким взяли, буквально из постели, убедились, что с галактическими языками у Вас не очень, согласно инструкции миссии просканировали Ваш мозг нейроспайдером, ну и из чистой любознательности загадали загадку. Отгадаешь, мол, — отпустим: «Наш корабль — он в виде тора, отсеки — сектора тора. Дверь вперед, дверь назад — все соединены. В отсеках включен свет, не во всех, а в случайном порядке. Можешь ходить по отсекам взад-вперед в любом направлении, можешь включать и выключать свет в любом отсеке сколько угодно раз. Требуется определить, сколько всего отсеков на корабле! Метить двери, отсеки мелом, пинком, разбитием лампочки или еще как нельзя.»
И вот, стоите Вы голый и ошарашенный босиком на холодном металлическом полу и озираетесь. Ни иллюминаторов, ни заметной кривизны стен или потолка, никаких косвенных признаков величины или направления кривизны тора не наблюдаете. Начинаете лихорадочно соображать, а можно ли, действительно, разгадать загадку, только включая и выключая свет в отсеках?
Домой-то хочется.

_{По мотивам…}