Задачи по геометрии

Построить равносторонний треугольник, одна вершина которого лежала бы на данной оружности, вторая на данной прямой, а третья в данной точке.

_{Б. Делоне, О. Житомирский}

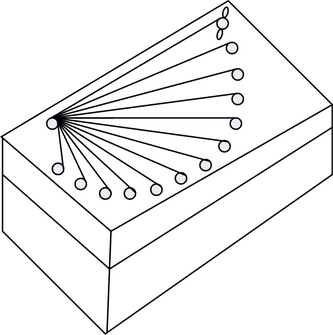
Цветик так красиво играл на флейте, что Незнайка твердо решил составить с ним дуэт и попросил Винтика и Шпунтика изготовить для него гусли, которые настраивались бы всего одной крутилкой, без хитростей и этих там всяких, как их, да, — камертонов, вот. Винтик взял обувную коробку, Шпунтик — рыболовную леску и набор карандашей, и работа закипела. В коробке насверлены отверстия, вставлены карандаши, а леска протянута так, что над крышкой она образует струны, а под крышкой прилегает к ее поверхности и не звучит. Пройдя от первого колка через все остальные, на последнем она подтягивалась и натяжение было одинаковым на всем ее протяжении, что и обеспечивало, собственно, настройку инструмента. Струны издавали звуки хроматической гаммы, т.е. звучали с интервалом в полутон, потому Незнайка гордо назвал новый инструмент «Хромогусли». По какой же системе расположили Винтик и Шпунтик карандаши-колки?

Говорят, что в катафотах, световозвращателях используется уголковый отражатель в виде примыкающих друг к другу трех взаимноперпендикулярных зеркал, как, например, внутренняя поверхность срезанной вершины куба. С какой бы стороны ни попал луч света на уголковый отражатель, отраженный луч уйдет точно в том же направлении, откуда пришел. Как это доказать?

_{Математические этюды}

Клоуны в перерыве между номерами играли за кулисами на бильярде. В пылу азарта один из них так ударил по шару, что шар вылетел со стола и, пробив бумажный колпак напарника, запрыгнул в горшок с пальмой, где и потерялся навеки. Расследуя обстоятельства пропажи шара, администратор цирка решил лично провести баллистическую экспертизу. Выполнив развертку пришедшего, заметьте, в негодность коническго колпака, администратор был весьма удивлен формой отверстий. И даже, что не характерно для администраторов, составил уравнение контура каждого отверстия. А вы можете повторить его подвиг?

Вне сферы радиуса R заданы точки А и С. Найти на cфере точку B, для которой сумма |AB|+|BC| минимальна.

Определите площадь треугольника ММК: Мадрид-Москва-Калькутта.

На карте указаны отрезки трёх прямолинейных дорог,
соединяющих три деревни, но сами деревни расположены за пределами
карты. Кроме того, на карте не указана пожарная часть, находящаяся
на равном расстоянии от трёх деревень, хотя место её расположения
находится в пределах карты. Можно ли найти это место с помощью
циркуля и линейки, если проводить построения только в пределах карты?

_{Фольклор}

Найти полуоси эллипса с фокусами в точках А и С, касающегося прямой f.

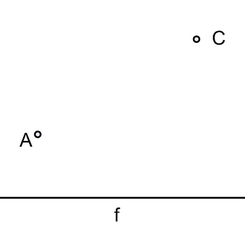
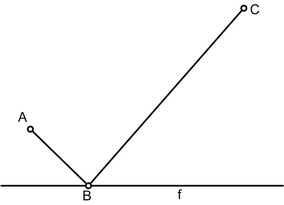
Найти такое положение точки B на прямой f, чтобы сумма отрезков |AB|+|BC| была минимальной.

_{Прислано пользователем Sabit}

С помощью циркуля и линейки восстановить треугольник по его описанной окружности и точкам (следам) M, B и H пересечения с ней продолжений медианы, биссектрисы и высоты, опущенных из одной вершины.

_{Из коллекции пользователя Sabit}

На плоскости имеются окружность и прямая произвольного положения. На прямой отмечена точка А. Построить окружность, касающуюся данной окружности и касающуюся данной прямой в точке А.

_{Из коллекции пользователя Sabit}