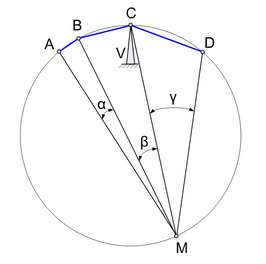
Задача № 156. Принесли его домой, оказался он… прямой!
Четверг, января 27, 2011В треугольнике ABC проведены высоты AD и BE, пересекающиеся в точке H. G — середина стороны AB. Прямые AB и DE пересекаются в точке F. Докажите, что прямые CF и GH перпендикулярны.
dxdy.ru