Задача № 263. На проспекте удвоения куба
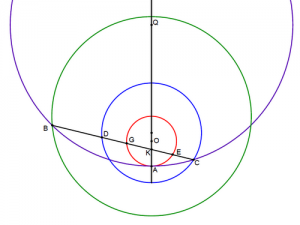
Воскресенье, февраля 26, 2017Проведем прямую AQ. С центром в точке O на ней построим окружность диаметром 3 так, что |AO|=1,5 (красная окружность). Отметим на прямой точку K так, что |AK|=1. Проведем через точку K под произвольным углом прямую, пересекающую окружность в точках G и E. Очевидно, в любом случае |GK|*|GE|=2. Построим с центром на прямой AQ окружность диаметром 17, касающуюся первой окружности в точке A (фиолетовая окружность). Пусть прямая GE пересекает вторую окружность в точках B и C. Очевидно, в любом случае |BK|*|CK|=16. Вращая прямую GE вокруг точки K можно найти такое ее положение, что |KE|=2^(1/3), а |GK|=2^(2/3), т.е. |GK|=|EK|^2. Вращая прямую BC вокруг точки K можно найти такое ее положение, что |KC|=2*2^(1/3), а |GE|=4*2^(2/3). С помощью гомотетии с коэффициентом 2 и центром в точке K построим синюю окружность. Точка C пересечения синей и фиолетовой окружности будет обладать замечательным свойством |KE|=|CK|=2^(1/3). Проверим наше построение с помощью окружности, полученной с помощью гомотетии с центром в точке K и коэффициентом 4 (зеленая окружность). На её пересечении с фиолетовой окружностью находится точка B такая, что |BK|=4*|GK|=4*2^(2/3), т.е. |BK|=|CK|^2. Легко убедиться, что точки B, K и E лежат на одной прямой.
Однако, почему не ликуют древние греки? Ведь мы построили отрезок, равный кубическому корню из 2, решив таким образом задачу об удвоении куба! Возможно, в наше построение вкралась ошибка? Найдите её.