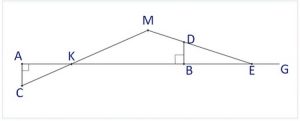
На прямой AG отмечен отрезок AB длиной 2a. Из точек А и B перпендикулярно прямой AG по разные её стороны проведены отрезки AC и BD, причем AC=BD=b.
Из точки C и точки D проведены отрезки СM и DM так, что CM пересекает AB, обозначим точку их пересечения через K, DM пересекает прямую AG вне отрезка AB, обозначим точку их пересечения через E, причем угол MKB равен углу MEB. Найти геометрическое место точек M (составить уравнение кривой).
На сколько частей делит пространство лента Мёбиуса бесконечной ширины?
С помощью циркуля и линейки построить окружность, касающуюся двух данных окружностей, причем одной из них в данной точке.
Город имеет форму круга радиуса R. По всей площади города магазины торговой сети расположены равномерно. Расстояние от центра города до распределительного центра сети равно r. Найти среднее расстояние от распределительного центра до магазина сети.
Квадрат ABCD и правильный пятиугольник BEFGC имеют общую сторону BC. Вершины квадрата A и D лежат вне пятиугольника. Найти угол между отрезками AG и FD.
Метеорит падает на сферическую Землю радиусом R под углом ѳ к отвесу со скоростью V и упруго (без потери энергии) отскакивает. В каком случае (при каком соотношении параметров) метеорит, попрыгав. вернётся в точку падения? (Допустим, g не меняется с высотой).
Е.Скляревский
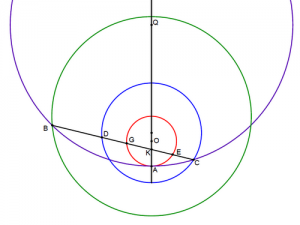
Проведем прямую AQ. С центром в точке O на ней построим окружность диаметром 3 так, что |AO|=1,5 (красная окружность). Отметим на прямой точку K так, что |AK|=1. Проведем через точку K под произвольным углом прямую, пересекающую окружность в точках G и E. Очевидно, в любом случае |GK|*|GE|=2. Построим с центром на прямой AQ окружность диаметром 17, касающуюся первой окружности в точке A (фиолетовая окружность). Пусть прямая GE пересекает вторую окружность в точках B и C. Очевидно, в любом случае |BK|*|CK|=16. Вращая прямую GE вокруг точки K можно найти такое ее положение, что |KE|=2^(1/3), а |GK|=2^(2/3), т.е. |GK|=|EK|^2. Вращая прямую BC вокруг точки K можно найти такое ее положение, что |KC|=2*2^(1/3), а |GE|=4*2^(2/3). С помощью гомотетии с коэффициентом 2 и центром в точке K построим синюю окружность. Точка C пересечения синей и фиолетовой окружности будет обладать замечательным свойством |KE|=|CK|=2^(1/3). Проверим наше построение с помощью окружности, полученной с помощью гомотетии с центром в точке K и коэффициентом 4 (зеленая окружность). На её пересечении с фиолетовой окружностью находится точка B такая, что |BK|=4*|GK|=4*2^(2/3), т.е. |BK|=|CK|^2. Легко убедиться, что точки B, K и E лежат на одной прямой.
Однако, почему не ликуют древние греки? Ведь мы построили отрезок, равный кубическому корню из 2, решив таким образом задачу об удвоении куба! Возможно, в наше построение вкралась ошибка? Найдите её.
Дана окружность с отмеченной на ней точкой А и точка В вне окружности. Найти параболу (построив ее директрису) с фокусом в точке В, касающуюся окружности в точке А.
В просторном зале, стоя на полу, вы видите на полу отражение светильника, подвешенного под потолком. Пусть ваш рост h, высота потолка H, расстояние между вами и точкой на полу под светильником S. Вы двигаетесь в направлении светильника со скоростью V. С какой скоростью вы догоняете отражение светильника? С какой скоростью отражение светильника движется к точке под светильником?
На плоскости построены два отрезка длинами a и b. С помощью циркуля и двух прямых углов (например, в виде школьных угольников) построить отрезки длинами c и d — два средних пропорциональных отрезка к данным a и b, т.е. чтобы выполнялось соотношение a:c = c:d = d:b.
Из точки, где плоскость, наклоненная под углом α к горизонту, сопрягается с горизонтальной плоскостью, выстрелили шариком под углом β к горизонту. Каким должен быть угол β, чтобы шарик, отскочив от наклонной плоскости, вернулся в точку выстрела?
Е. Скляревский
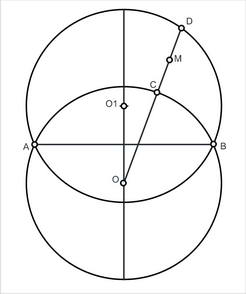
Две окружности равного радиуса с центрами в точках О и О1 имеют общую хорду АВ. Из точки О проведен в произвольном направлении отрезок, пересекающий хорду AB, затем пересекающий окружность O в точке С и окружность О1 в точке D. Пусть М – середина отрезка CD. Доказать (или опровергнуть), что геометрическим местом точек M является дуга окружности.
Дана окружность и в ней центральный острый угол альфа. Построить угол, равный третьей части альфа, используя циркуль и линейку, на которой можно делать засечки, так, чтобы все построения не выходили за пределы окружности.
В горизонтальной плите имеются два параллельных желоба полукруглого сечения радиуса R. Центры полукружий находятся в плоскости поверхности плиты на расстоянии L<2R друг от друга. На краю одного из желобов установлен шарик радиуса r. Шарик скатывается в желоб. При каком максимальном L шарик перескочит из одного желоба в другой? Трение отсутствует.
На наклонной плоскости два ткача придерживают два совершенно одинаковых рулона ткани. Одновременно отпускают. Один рулон скатывается со склона как цельный цилиндр, а второй во время спуска разматывается. Скольжение отсутствует. Какой рулон скатится быстрее?
