На плоскости начерчены две пересекающиеся окружности радиусов r1 и r2. Можно ли с помощью циркуля и линейки провести третью окружность заданного радиуса r3 так, чтобы она проходила через точку пересечения двух первых и отсекала на них дуги, стягиваемые равными хордами?
На плоскости лежат, касаясь друг друга, два шара радиусов R и r. Найти геометрическое место центров шаров, касающихся двух данных. Интересно составить уравнение кривой пересечения ГМТ с опорной плоскостью шаров. Если ГМТ разбивает пространство на два полупространства, можно ли оценить отношение частей объема «меньшего» из них, на которые разбивает его опорная плоскость?
В большом неподвижном колесе R водило V длиной R/2 начинают вращать вокруг центра O с угловым ускорением ε до поворота его на 180 градусов, после чего вращение замедляют с тем же ускорением до остановки его в начальной точке. При этом малое колесо R/2, ось вращения которого находится на конце водила в точке Q, катится по большому благодаря зубчатому зацеплению. В точке контакта колес перед началом движения K на оси, расположенной на малом колесе, подвешена (с возможностью вращения вокруг этой оси) спецлюлька, куда инкапсулирован космонавт. Какую максимальную перегрузку испытает космонавт?
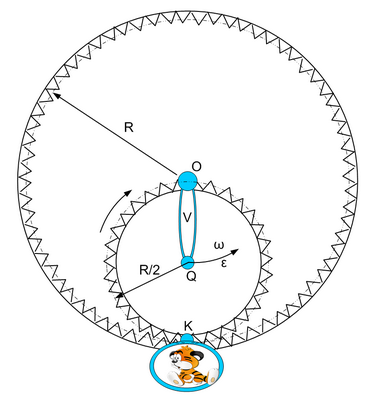
в процессе испытаний все были пристегнуты ремнями безопасности, и никто не пострадал
Вот среди ночи тайком взяли Вы, к примеру, конус из детского набора деревянных фигур и из баловства, ну вот буквально от нечего делать, не задумываясь, начертили у него на боку циркулем «окружность». Ну и конечно же заметили, что окружность какая-то не круглая. И на развертке конуса не круглая. И вообще никак не круглая. И решили составить уравнение этой кривулины на развертке конуса. Вот и мучайтесь! Да. А я спать пошел. 🙂
Дан отрезок AB, на котором выбрана точка L. Найти геометрическое место вершин С треугольников ABC, для которых CL — биссеткриса угла ACB.
В треугольнике АВС АС=(АВ+ВС)/2. Докажите, что центр вписанной в треугольник АВС окружности, середины сторон АВ и ВС и вершина В лежат на одной окружности.
По неподвижному эллипсу катится без скольжения равный ему эллипс так, что в каждый момент времени они симметричны относительно общей касательной. Какие линии описывают фокусы движущегося эллипса?
На стороне AD внутри квадрата ABCD построен равносторонний треугольник A’D’E. Треугольник поворачивается так, что его вершина A’ скользит по стороне квадрата от A к D, а вершина D’ скользит по стороне квадрата от D к C. Какую кривую, непрерывно её касаясь, огибает при этом основание A’D’ треугольника? По каким кривым движутся центр O и вершина E треугольника?
Имеются две скрещивающиеся под углом А прямые, расстояние между которыми составляет a. Шар радиуса R>a касается обеих прямых. Найти геометрическое место всех точек, в которых может находиться центр шара.
Найти плоскую фигуру наименьшей площади, внутри которой возможен поворот равностороннего треугольника на 360 градусов.
Мишаня Дундило
Мастер спорта международного класса по спортивной гимнастике Бруно Альбертович Циглер, разучивая с подопечными на тренировке по акробатике новый элемент, для иллюстрации правильного положения головы в полёте прикрепил за ухом ручку-указку с лазерным лучом так, чтобы луч лазера совпадал с направлением взгляда прямо перед собой. Итак, разбег, рандат – фляк – сальто назад прогнувшись с пируэтом в 360 градусов, блестяще исполненное приземление без доскока и лишних шагов. Акробатическая дорожка пролегла вдоль средней линии спортзала, представляющего собой параллелепипед. Попробуйте изобразить траекторию следа лазерного луча на внутренней поверхности спортзала при выполнении сальто.
Ёмкость автотопливозаправщика представляет собой цилиндр, имеющий в поперечном сечении эллипс с полуосями a и b. Ёмкость заполнена частично, уровень топлива h от дна ёмкости. Какую кривую огибает уровень топлива на поворотах? Какую кривую огибает уровень топлива при разгоне и торможении на прямолинейных участках дороги, если длина ёмкости l ? (Волнением топлива пренебрегаем, считаем поверхность плоской).
На вертикально установленной доске в точках A и B закреплены концы нити длиной l > AB. Отрезок AB образует острый угол a с вертикалью. Надетое на нить кольцо в состоянии равновесия находится в точке C. Найти отношение, в котором кольцо делит нить. Массой нити пренебречь. (Рассмотреть два варианта: 1) кольцо свободно скользит по нити; 2) кольцо закреплено на нити.)
Из коллекции validolum
Даны три пересекающиеся плоскости, не имеющие общей прямой. Найти геометрическое место таких точек, сумма расстояний от которых до данных плоскостей постоянна.
И.Ф. Шарыгин
Можно ли найти эллипс с таким эксцентриситетом е, при котором площадь, ограниченная эволютой эллипса, равна площади эллипса?
