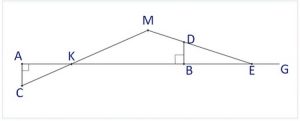
На прямой AG отмечен отрезок AB длиной 2a. Из точек А и B перпендикулярно прямой AG по разные её стороны проведены отрезки AC и BD, причем AC=BD=b.
Из точки C и точки D проведены отрезки СM и DM так, что CM пересекает AB, обозначим точку их пересечения через K, DM пересекает прямую AG вне отрезка AB, обозначим точку их пересечения через E, причем угол MKB равен углу MEB. Найти геометрическое место точек M (составить уравнение кривой).
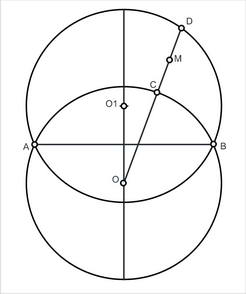
Две окружности равного радиуса с центрами в точках О и О1 имеют общую хорду АВ. Из точки О проведен в произвольном направлении отрезок, пересекающий хорду AB, затем пересекающий окружность O в точке С и окружность О1 в точке D. Пусть М – середина отрезка CD. Доказать (или опровергнуть), что геометрическим местом точек M является дуга окружности.
Точки A и B подвеса концов невесомого нерастяжимого каната длиной L находятся на неподвижных опорах высотой Ha и Hb, расстояние между основаниями опор по горизонтали равно с. Нетрудно найти траекторию движения канатоходца, идущего по такому канату. Но какова будет траектория движения канатоходца массой m по канату массой M при тех же условиях подвеса каната?
Дан треугольник ABC с длинами сторон BC=a, AC=b, AB=c. Прямые l1 и l2, образующие угол d, делят его на три равновеликие части. Найти геометрическое место вершин угла d.
Николай Москвитин
В горизонтальной плоскости P расположены две взаимно перпендикулярные прямые x и y, пересекающиеся в точке O. В вертикальной плоскости V, перпендикулярной биссектрисе угла между прямыми x и y и содержащей точку O, расположена окружность радиуса a, касающаяся плоскости P в точке O. В плоскости V также расположена концентричная первой окружность радиуса a-1. Окружности, оставаясь вертикальными и концентрическими, начинают перемещаться в направлении биссектрисы угла между x и y так, что большая окружность все время касается прямых x и y. Какую кривую образуют точки пересечения малой окружности с плоскостью P? Найти её уравнение.
Из крана периодически капает вода, капли падают вертикально в воду в бассейне, вертикальная стенка которого находится на расстоянии а от линии падения капель. При падении капля выбивает брызги с поверхности воды. Допустим, брызги разлетаются всегда под углом b к поверхности воды. Какую кривую образуют на стенке бассейна точки падения брызг на неё?
Какую кривую (семейство кривых) описывает в течение года тень верхушки Ташкентской телебашни высотой 375 м?
Е. Скляревский
На горизонтальной прямой установлены в вертикальной плоскости, содержащей данную прямую, три окружности радиусов R1, R2 и R3, имеющие общую точку касания между собой и с прямой. Данную точку помечают на прямой как A, на окружностях соответственно A1, A2 и A3. В некоторый момент времени все три окружности начинают катиться по прямой без скольжения в одну сторону с одинаковой для всех трех окружностей и постоянной угловой скоростью w. Доказать, что при этом в любой момент времени точки A, A1, A2 и A3 находятся на одной прямой. Найти зависимость наклона этой прямой к горизонту от времени.
«Увидел Садко: во синем море
Стоит палата белокаменная.»
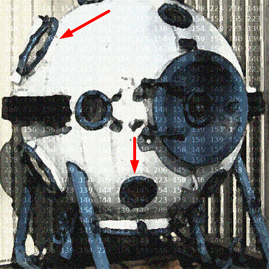
Лампа внутреннего освещения в батисфере диаметром D расположена в её верхней полюсной точке. В боковой поверхности верхней полусферы имеется круглый иллюминатор диаметром d1, а в боковой поверхности нижней полусферы — диаметром d2. Ось верхнего иллюминатора наклонена под 45° к горизонту, а нижнего — под 60°. Батисфера встала на горизонтальном участке дна на шасси так, что нижняя полюсная точка сферы оказалась на высоте h над дном. Какую форму и размеры будут иметь световые пятна на дне от лучей, проходящих через иллюминаторы?
Толщиной стенок, преломлением, рефракцией и рассеянием света Садко пренебрег, ну и мы тоже.
Коля и Петя из хулиганских исследовательских побуждений взяли трубу квадратного сечения за торцы и скрутили, повернув торцы друг относительно друга на 720 градусов. Ось трубы при этом осталась прямолинейной. Трубу прокатили по песку в направлении, перпендикулярном ее оси, слегка придавив её и сделав несколько оборотов, так, что вдоль её траектории не осталось не тронутых трубой участков песка. Попробуйте построить сечения следа на песке в направлении движения трубы и в направлении, параллельном оси трубы.
Цилиндрический ролик длиной L и диаметром D катится по горизонтальной плоскости без проскальзываний. В некоторый момент времени диаметр одного из оснований цилиндра начинает меняться пропорционально углу поворота ролика вокруг своей оси (при этом прямолинейность образующей сохраняется, т.е. ролик становится усеченным конусом) и уменьшается за два оборота ролика вокруг своей оси от D до нуля. Какую траекторию опишет на плоскости точка касания малого основания ролика к плоскости?
Во внутренней полости конуса с вертикальной осью и углом при вершине A на высоте H от вершины конуса вдоль его внутренней поверхности под углом к горизонтали B запускают шарик радиуса r с начальной скоростью v. Трение между конусом и шариком отсутствует, поверхности конуса и шарика абсолютно тверды. Какова будет траектория шарика?
Е.Скляревский
К вертикальной стороне прямого угла с внутренней стороны примыкает диаметром полуокружность, находящаяся в плоскости этого прямого угла. На полуокружности выбрана произвольная точка С. Нижний конец А диаметра начинает скольжение вдоль горизонтальной стороны угла, а верхний конец B диаметра — вдоль вертикальной стороны угла, при этом полуокружность остаётся в плоскости угла. По какой траектории движется точка С?
На стороне остроугольного треугольника обнаружить такую точку M, из которой луч света, пущенный под некоторым углом, отразившись последовательно от двух других сторон треугольника, вернулся бы в исходную точку M.
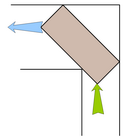
Петя Васильчиков — гениальный ребенок. Так полагает его бабушка Элеонора Бельц. Разумеется, каждый гениальный ребенок просто обязан стать гениальным пианистом. «Только Ronisch 132 !» – настаивала бабушка под самый Новый год. И вот, грузчики Михалыч и Пахомыч пытаются мимо наряженной ёлки закатить пианино в Петину комнату. Для этого им необходимо преодолеть поворот коридора. Ширина коридора до поворота 130 см, длина пианино 152 см, ширина 63 см. Известно, что слегка зацепив обои, но не поцарапав при этом инструмент, грузчики справились с задачей. Какова же была ширина коридора после поворота? Да, интересно также, какой формы следы оставили на полу колеса пианино весом 235 кг.
фольклор
