Задачи по геометрии

Квадрат ABCD и правильный пятиугольник BEFGC имеют общую сторону BC. Вершины квадрата A и D лежат вне пятиугольника. Найти угол между отрезками AG и FD.

_{http://blog.kknop.com/2017/03/blog-post.html}

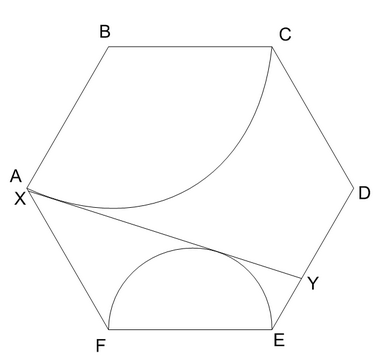
Внутри правильного шестиугольника ABCDEF построена дуга AC с центром в B, а на EF как на диаметре построена полуокружность. Общая касательная дуги и полуокружности пересекает AF в точке X, а DE в точке Y. Найти длину отрезка XY.

_{mathisfunforum.com}

Диагонали произвольного вписанного четырехугольника ABCD пересекаются в точке P. Доказать, что AB*BC*PD=AD*DC*PB.

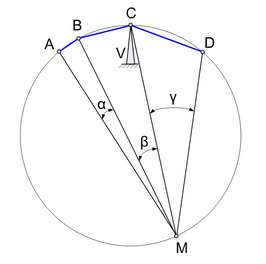
На окружности радиуса R отмечены последовательно точки A, B, C, D, M. На дугу AB опирается угол α, на дугу BC — угол β, на дугу CD — угол γ. Ломаную вдоль хорд ABCD выполнили из проволоки постоянного сечения и установили точкой C на рычажные весы V. Если α и β известны, при каком угле γ проволока будет находиться в равновесии? Зависит ли γ от R?

Суммарный объем двух кубиков равен 17. Не могли бы Вы указать их точные размеры?

_{По следам Домашнего задания}

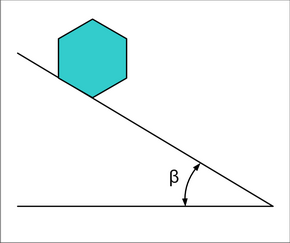
На плоскость, наклоненную к горизонту под углом бета, кладут монолитную шестигранную прямоугольную призму так, что её продольная ось параллельна горизонту, и отпускают. Случись покатившейся призме подпрыгнуть или, приземлившись, удариться о плоскость, удар будет абсолютно упругим. Скольжение между плоскостью и призмой отсутствует. Найдется ли такой угол бета, при котором покатившаяся и ненароком оторвавшаяся от плоскости призма приземлится на наклонную плоскость точно какой-либо из своих боковых граней (ну то есть не ударится о неё ребром, высекая искры, а шлёпнется всей боковой гранью плашмя)?

Длины сторон четырёхугольника, описанного около окружности радиуса R, взятые последовательно, образуют геометрическую прогрессию. Найти площадь четырёхугольника.

_{И.Ф. Шарыгин, Задачи по геометрии, М. «Наука», 1982}

Построить правильный 5-угольник по 5 точкам на его сторонах.

_{Задача предложена Jan в комментариях к задаче № 22.}