Архив на категорию ‘площадь’
Пятница, апреля 21, 2017
Город имеет форму круга радиуса R. По всей площади города магазины торговой сети расположены равномерно. Расстояние от центра города до распределительного центра сети равно r. Найти среднее расстояние от распределительного центра до магазина сети.
Категория: Задачи на вычисление, площадь, Подумалось вдруг, этюды | Нет комментариев »
Вторник, марта 4, 2014
В прямоугольной системе Декартовых координат дано семь точек: A(0;0); B(0;2); C(1;4); D(3;5); E(5;4); F(6;2); G(6;0). Назовём семиугольник ABCDEFG «холмом». Требуется разрезать его на 9 частей, чтобы из них можно было составить четыре квадрата с площадями 9,9,5,1.
М. Москвитин, А.Заславский
P.S. Найдены решения разбивки и на 8 частей для получения того же результата. Может быть, удастся найти решение и с 7-ю частями?
Категория: задачи на разрезание, квадрат, площадь | 1 Комментарий »
Понедельник, октября 28, 2013
Диагональ делит ромб со стороной а на два треугольника, в которые вписаны окружности. Вторая диагональ также делит ромб на два треугольника и в них тоже вписаны окружности. При каком отношении диагоналей сумма площадей всех четырех окружностей будет наибольшей?
Е. Скляревский
Категория: Задачи на вычисление, площадь, четырехугольник, этюды | 1 Комментарий »
Среда, августа 14, 2013
Две окружности радиусов R (большая) и r (малая) имеют общую хорду AB. В малой окружности проведена хорда BC=AB. Известно, что площадь малого сегмента большой окружности, стягиваемого хордой AB, равна площади треугольника, составленного из хорд AB, BC и дуги AC малой окружности. В каком отношении находятся площади двух частей, на которые большая окружность разбивает малую?
Категория: Задачи на вычисление, задачи на разрезание, площадь, Подумалось вдруг | Нет комментариев »
Вторник, июня 4, 2013
Найти центр тяжести фигуры, ограниченной последним витком логарифмической спирали вида r=ae^(bφ) и отрезком AB радиального луча OB.
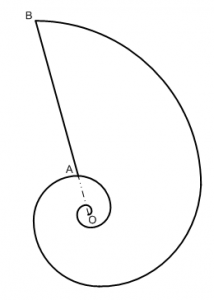
Категория: Задачи на вычисление, Замечательные кривые, площадь, Подумалось вдруг, этюды | Нет комментариев »
Суббота, июня 1, 2013
Куб А со стороной 1 метр повернули на 45 градусов вокруг основной диагонали и получили куб Б. Найти площадь поверхности фигуры, оказавшейся в пересечении кубов А и Б.
Квант
Дополним для остроты: и объем!
🙂
Категория: Задачи на вычисление, площадь, Стереометрия | Нет комментариев »
Среда, февраля 27, 2013
На плоскости задан отрезок единичной длины. С помощью только циркуля построить фигуру площадью Пи/3+sin(Пи/3).
Категория: Задачи на вычисление, Задачи на построение, площадь, Подумалось вдруг, этюды | 2 Комментариев »
Четверг, января 31, 2013
Через произвольно отмеченную на стороне треугольника точку провести прямую, делящую площадь треугольника в заданном отношении m/n.
Категория: Задачи на построение, задачи на разрезание, площадь, Подумалось вдруг, треугольник | Нет комментариев »
Вторник, декабря 18, 2012
В кружке диаметром d поверх кофе не смешивающийся с ним слой сливок. На сколько градусов нужно наклонить кружку, чтобы слой сливок стал вдвое тоньше? Какой уровень кофе в кружке должен был быть первоначально, чтобы при требуемом наклоне не обнажилось дно? Какой высоты должна быть кружка, чтобы при требуемом наклоне ни капли сливок не пролилось?
по следам Инфобума
Категория: Задачи на вычисление, Замечательные кривые, конус, Объём, площадь, Стереометрия, цилиндр, Эллипс | 2 Комментариев »
Воскресенье, сентября 2, 2012
В треугольнике ABC проведены чевиана BD, описанные окружности треугольников ABD и CBD с центрами O1 и O2 соответственно, высота BE. Доказать: площадь четырёхугольника EO1BO2 равна половине площади треугольника ABC.
Николай Москвитин
Категория: задачи на доказательство, площадь, треугольник, четырехугольник | Нет комментариев »
Пятница, апреля 1, 2011
Через произвольно выбранную точку М внутри треугольника провести прямую, разрезающую треугольник на две равновеликие фигуры.
webmath.ru
Категория: Задачи на построение, задачи на разрезание, площадь, треугольник | 2 Комментариев »
Суббота, марта 26, 2011
На стороне АС равнобедренного треугольника АВС (АВ=ВС) как на диаметре построена окружность, пересекающая АВ в точке Е. Медиана АD и отрезок СЕ пересекаются в точке Р. Найти площадь треугольника АВС, если РС=7, РЕ=3.
webmath.ru
Категория: Задачи на вычисление, площадь, треугольник | 4 Комментариев »
Пятница, декабря 17, 2010
Стороны и высота треугольника выражаются четырьмя последовательными целыми числами. Чему равна площадь этого треугольника?
Г.Э. Дьюдени
Категория: Задачи на вычисление, Классика, площадь, треугольник | 1 Комментарий »
Четверг, ноября 25, 2010
Каким минимальным числом полос изоленты шириной 1 см можно обклеить куб с ребром N см, использовав при этом минимальное количество изоленты, если ленты можно клеить только параллельно ребрам куба?
Е. Скляревский. По следам problems.ru
Категория: Задачи на вычисление, Куб, площадь | 4 Комментариев »
Вторник, ноября 9, 2010
Радиус купола R, коэффициент трения лапок птиц о купол k. Сколько птиц поместится на куполе, если одна птица занимает площадь S? Еще надо уточнить, что птички — неделимые, недеформируемые кружки площадью S.

Е.С. Скляревский Компот
Категория: Задачи на вычисление, Механические утехи, около физики, площадь, этюды | Нет комментариев »

