Метеорит падает на сферическую Землю радиусом R под углом ѳ к отвесу со скоростью V и упруго (без потери энергии) отскакивает. В каком случае (при каком соотношении параметров) метеорит, попрыгав. вернётся в точку падения? (Допустим, g не меняется с высотой).
Е.Скляревский
Дана окружность с отмеченной на ней точкой А и точка В вне окружности. Найти параболу (построив ее директрису) с фокусом в точке В, касающуюся окружности в точке А.
Из точки, где плоскость, наклоненная под углом α к горизонту, сопрягается с горизонтальной плоскостью, выстрелили шариком под углом β к горизонту. Каким должен быть угол β, чтобы шарик, отскочив от наклонной плоскости, вернулся в точку выстрела?
Е. Скляревский
Пушка стреляет, меняет угол наклона на 1 градус, снова стреляет, пока не обойдет 360 градусов (пушка приподнята над землей). Найти линию, огибающую все траектории снарядов.
Е.Скляревский
Шарик падает с высоты h на наклонную плоскость и прыгает по ней. Как зависит период прыжков от угла наклона плоскости а? Потерями на трение и соударения пренебречь.
Е.Скляревский
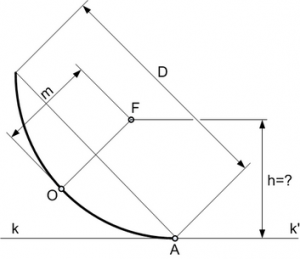
Параболическую антенну диаметром D с фокусным расстоянием OF=m расположили на горизонтальной плоскости kk’ так, что в точке A, принадлежащей диаметру D, парабола касается плоскости kk’. На какой высоте от плоскости kk’ оказался фокус параболы F ?
Парабола задана на плоскости фокусом и директрисой. На той же плоскости отмечены произвольно точки P и Q. С помощью циркуля и линейки найти точки пересечения параболы и прямой.
Авто поднято на подъемнике. От пола до днища картера 180 см. Ось маслосливной горловины наклонена к вертикали под 45°. На полу оцинкованное ведро посреди кучки опилок. Ловким движением туфли мастер устанавливает ведро так, что при съеме пробки масло точно попадает в ведро, и потом в процессе туфля пододвигает ведро еще пару раз. Можно ли сразу установить ведро так, чтоб пододвигать в процессе не приходилось до полной кончины масла, если высота и диаметр верхнего среза ведра равны 30 см, а глубина масла в картере 10 см?
Антенщик-мачтовик, монтируя что-то там на 500-метровой отметке Останкинской телебашни, выронил гайку. В какую сторону и на сколько метров будет отстоять точка падения гайки на землю от вертикали, проходящей через начальную точку?
фольклор
Мячик скатывается под действием силы тяжести по обрезанному параболическому трамплину y(x)=(x-a)^2+b — находясь в начальный момент в точке x=0 y=a^2+b, a и b>0 — определить в какой точке обрезать параболу, чтоб дальность полета была максимальной.
YuK
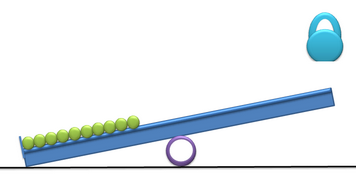
Двухметровая доска лежит на асфальте одним концом, середина доски опирается на трубу. На конце доски буртик, в который упираются уложенные в продольный желобок доски в ряд десять теннисных мячей. Угол наклона доски в первоначальном состоянии 20 градусов к горизонту. На второй конец доски с высоты 1 метр бросают пудовую гирю. На каком расстоянии друг от друга приземлятся мячи?
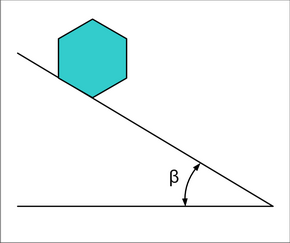
На плоскость, наклоненную к горизонту под углом бета, кладут монолитную шестигранную прямоугольную призму так, что её продольная ось параллельна горизонту, и отпускают. Случись покатившейся призме подпрыгнуть или, приземлившись, удариться о плоскость, удар будет абсолютно упругим. Скольжение между плоскостью и призмой отсутствует. Найдется ли такой угол бета, при котором покатившаяся и ненароком оторвавшаяся от плоскости призма приземлится на наклонную плоскость точно какой-либо из своих боковых граней (ну то есть не ударится о неё ребром, высекая искры, а шлёпнется всей боковой гранью плашмя)?
Составить из дуг парабол криволинейный треугольник наименьшей площади с заданными вершинами (стороны треугольника должны пересекаться только в вершинах и быть направлены выпуклостью внутрь).
Лаборант Михалыч вынул пробку, и тут ему позвонили. На столе образовалась лужа глубиной около 1. Оцените форму лужи.
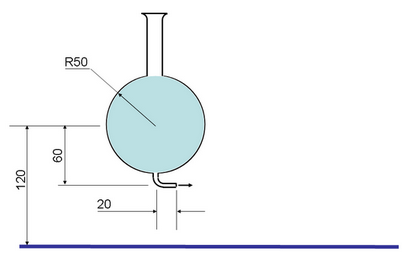
Из объяснительной Михалыча впоследствии выяснилось, что пробка была диаметром 5.
Параболу у=(1/360)х2 повернули на (1/360)° вокруг начала отсчёта. Пересечёт ли она положительную полуось ординат?
