Архив на категорию ‘Эллипс’
Вторник, декабря 18, 2012
В кружке диаметром d поверх кофе не смешивающийся с ним слой сливок. На сколько градусов нужно наклонить кружку, чтобы слой сливок стал вдвое тоньше? Какой уровень кофе в кружке должен был быть первоначально, чтобы при требуемом наклоне не обнажилось дно? Какой высоты должна быть кружка, чтобы при требуемом наклоне ни капли сливок не пролилось?
по следам Инфобума
Категория: Задачи на вычисление, Замечательные кривые, конус, Объём, площадь, Стереометрия, цилиндр, Эллипс | 2 Комментариев »
Воскресенье, мая 30, 2010
Доказать, что если точку пересечения касательных к эллипсу в концах хорды, содержащей фокус, соединить с этим фокусом, получившаяся прямая будет перпендикулярна хорде.
А. В. Акопян, А. А. Заславский
Категория: задачи на доказательство, Замечательные кривые, Эллипс | Нет комментариев »
Вторник, апреля 20, 2010
Солнце в зените. На горизонтальной плоскости стоит вертикально круглый тонкий обруч диаметром D. Обруч начинает падать. Тень от обруча превращается в эллипс. Вы надеваете волшебные очки и видите, как сближаются фокусы эллипса. Шмяк! Обруч улегся горизонтально, фокусы слились в центре, волшебство исчезло. Допустим, обруч заваливался на бок с постоянной угловой скоростью w. Каков же был закон сближения (относительного движения) фокусов? А если обруч потерял равновесие и падал на бок под действием силы тяжести?
Категория: Задачи на вычисление, Механические утехи, Подумалось вдруг, Эллипс, этюды | Нет комментариев »
Воскресенье, января 10, 2010
По неподвижному эллипсу катится без скольжения равный ему эллипс так, что в каждый момент времени они симметричны относительно общей касательной. Какие линии описывают фокусы движущегося эллипса?
Математические олимпиады ОмГУ
Категория: геометрическое место точек, Задачи на построение, Замечательные кривые, Механические утехи, Эллипс | 3 Комментариев »
Суббота, ноября 28, 2009
Ёмкость автотопливозаправщика представляет собой цилиндр, имеющий в поперечном сечении эллипс с полуосями a и b. Ёмкость заполнена частично, уровень топлива h от дна ёмкости. Какую кривую огибает уровень топлива на поворотах? Какую кривую огибает уровень топлива при разгоне и торможении на прямолинейных участках дороги, если длина ёмкости l ? (Волнением топлива пренебрегаем, считаем поверхность плоской).
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, Механические утехи, Объём, площадь, Подумалось вдруг, Эллипс, этюды | 1 Комментарий »
Четверг, октября 8, 2009
Можно ли найти эллипс с таким эксцентриситетом е, при котором площадь, ограниченная эволютой эллипса, равна площади эллипса?
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, площадь, Подумалось вдруг, Эллипс, этюды | Нет комментариев »
Вторник, июля 14, 2009
Вписать эллипс в заданный параллелограмм.
Проблема любителей AutoCad и не только:)
Категория: Замечательные кривые, четырехугольник, Эллипс, этюды | Нет комментариев »
Среда, мая 20, 2009
Точка Q пересечения диагоналей вписанного в эллипс четырехугольника ABCD делит пополам хорду EF эллипса. EF пересекает стороны AB и CD четырехугольника в точках M и N соответственно. Можно ли доказать, что отрезки MQ и NQ равны?
Категория: Подумалось вдруг, четырехугольник, Эллипс, этюды | Нет комментариев »
Суббота, марта 7, 2009
Найти полуоси эллипса с фокусами в точках А и С, касающегося прямой f.
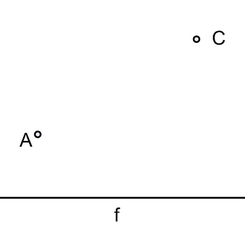
Категория: Задачи на построение, Подумалось вдруг, Эллипс, этюды | 2 Комментариев »
Среда, декабря 17, 2008
Вариация на тему задачи №5.
Прямой угол поворачивается вокруг эллипса, неотрывно касаясь эллипса обеими сторонами. Какую кривую описывает вершина угла?
Категория: Механические утехи, Эллипс | 4 Комментариев »
Понедельник, декабря 15, 2008
Имеется круг, вырезанный из листа бумаги. На нём отмечена точка, отличная от центра. Изобразите на круге эллипс.
Категория: Эллипс | 2 Комментариев »
Суббота, декабря 13, 2008
Эллипс поворачивается, касаясь обеих сторон прямого угла. Какую кривую описывают фокусы эллипса? По какой линии перемещается центр эллипса? Какую кривую описывает точка пересечения нормалей к эллипсу, проведенных через точки касания сторон угла? А если угол не прямой?
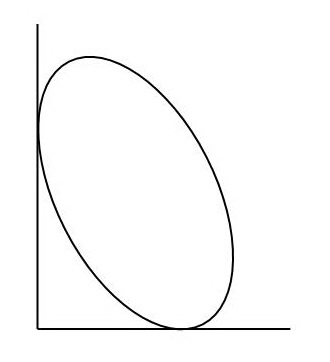
Категория: Механические утехи, Эллипс, этюды | 10 Комментариев »
Понедельник, ноября 17, 2008
Можно ли эллипс с эксцентриситетом е установить на плоскости, наклоненной под углом w к горизонту, так, что эллипс останется неподвижен?
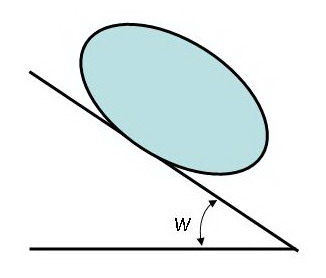
Теги: Эллипс
Категория: Замечательные кривые, Механические утехи, около физики, Подумалось вдруг, экстремумы, Эллипс, этюды | Нет комментариев »


