»

Задача № 1. Вариатор и его ремень.

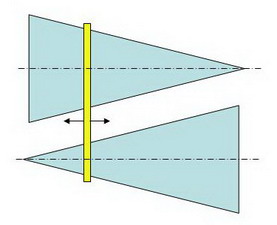
Всем знакомый с детства вариатор. Два конических вала, ремень… Изменяется ли натяжение ремня при его перемещении? Если да, то какой формы должны быть валы (вместо конических), чтобы натяжение (соответственно и длина) ремня оставалось постоянным?

d0b2d0b0d180d0b8d0b0d182d0bed180

Теги: ,

Эта запись опубликована Суббота, ноября 15, 2008 в 19:46 и находится в категории: Механические утехи, Подумалось вдруг. Вы можите читать эту запись через RSS 2.0 поток. Вы также можите оставить комментарий, или поставить trackback со своего сайта.

8 Комментарев на “Задача № 1. Вариатор и его ремень.”

  1. b_a_lamut сказал:
    декабря 18, 2008 - 03:50

    Эх, рассказали бы уже, какими должны быть валы >:)

  2. admin сказал:
    декабря 18, 2008 - 09:07

    Ха! Если б я знал:) Пока сам не решил ещё.

  3. b_a_lamut сказал:
    декабря 18, 2008 - 14:20

    Пока нет картинки, попробую объяснить на пальцах 🙂

    Например, конусы на твоём чертеже имеют размеры: длина -100 мм, а основание — 50мм

    Допустим, что конусы прилегают друг к другу (валы, естественно, временно не вращаются)

    Тогда ремень, в крайнем положении будет равен длине окружности одного из оснований, т.е. — 157 мм.
    Попытаемся переместить ремень в середину. Ничего не получится 🙁
    Если посмотреть на конструкцию сверху, то увидим, что в середине самое узкое место, но не верь глазам своим, лучше всё посчитать.

    В середине, ремень должен оказаться на двух одинаковых окружностях диаметром 25 мм каждая. Облегать он должен ровно по половине поверхности каждой окружности, т.е., длина облегания равна 78,5 мм. Длина в четыре радиуса этих окружностей не касается валов.

    Всё складываем и в результате получаем длину ремня равную 178.5 мм, что несколько больше, чем длина ремня с краёв вариатора.

    Вывод: в каждом конусе необходимо сделать выборку от центра к краям, подогнав размер ремня так, чтобы, всё, что соприкасается с валами и то, что находится в воздухе, равнялось 157 мм. Т.е., конусы должны иметь вогнутую поверхность >:)

  4. admin сказал:
    декабря 19, 2008 - 00:29

    честно, я пытался решить эту задачу, составил выражение для длины ремня L в зависимости от параметров: R — наибольший радиус, а — угол при вершине конуса, p — расстояние между осями конусов, х — смещение ремня от основания одного из конусов. И собирался исследовать ее методами матанализа, найти области возрастания-убывания, экстремумы и т.д. Но для изменения формы это ничего не даст, поскольку форма тут задана углом при вершине конуса. Выход вижу следующий: составить выражение для разности между L в начальном положении и L для текущего смещения ремня х, после чего для данных параметров R, a и p, оставив один из конусов в том же виде, найти такой радиус r второго тела вращения при текущем х, чтобы L текущее сравнялось с L начальным, получив таким образом уравнение образующей второго тела вращения. Надо бы, но пока руки не дошли:)

  5. b_a_lamut сказал:
    декабря 21, 2008 - 03:21

  6. b_a_lamut сказал:
    декабря 21, 2008 - 03:26

    Мдааа… Необходимо оговорить, что картинка не должна превышать 350 пикселей в ширину 🙁

  7. Костя сказал:
    ноября 23, 2016 - 00:50

    Куда бы он не перемещался, натяжение не изменится. Очевидный параллелограмм. Чтоб натяжение оставалось постоянным необходимо сохранить параллельность крайних сторон. Если конечно я все правильно понял)))

  8. balu сказал:
    февраля 6, 2017 - 22:23

    Боюсь, Костя, Вы ошибаетесь. Во всяком случае, попробуйте доказать Ваше утверждение. 🙂

Оставить комментарий