Задачи по геометрии

Квадрат ABCD и правильный пятиугольник BEFGC имеют общую сторону BC. Вершины квадрата A и D лежат вне пятиугольника. Найти угол между отрезками AG и FD.

_{http://blog.kknop.com/2017/03/blog-post.html}

Дана окружность (центр не отмечен). С помощью только циркуля построить вершины квадрата, вписанного в эту окружность.

В прямоугольной системе Декартовых координат дано семь точек: A(0;0); B(0;2); C(1;4); D(3;5); E(5;4); F(6;2); G(6;0). Назовём семиугольник ABCDEFG «холмом». Требуется разрезать его на 9 частей, чтобы из них можно было составить четыре квадрата с площадями 9,9,5,1.

_{М. Москвитин, А.Заславский}

P.S. Найдены решения разбивки и на 8 частей для получения того же результата. Может быть, удастся найти решение и с 7-ю частями?

Вокруг квадрата ABCD описана окружность с центром О, на дуге AB (меньшей) отмечена точка E, прямая EO пересекает окружность в точке F, середины отрезков CE и BC — точки K и L соответственно. Доказать: диагональ квадрата AC, отрезки FK и DL пересекаются в одной точке.

_{Н. Москвитин}

Коля и Петя из хулиганских исследовательских побуждений взяли трубу квадратного сечения за торцы и скрутили, повернув торцы друг относительно друга на 720 градусов. Ось трубы при этом осталась прямолинейной. Трубу прокатили по песку в направлении, перпендикулярном ее оси, слегка придавив её и сделав несколько оборотов, так, что вдоль её траектории не осталось не тронутых трубой участков песка. Попробуйте построить сечения следа на песке в направлении движения трубы и в направлении, параллельном оси трубы.

На отрезке AG произвольно выбрана точка D и на полученных отрезках как на сторонах построены квадраты ABCD и DEFG с вершинами по одну сторону от отрезка. Доказать, что середина отрезка BF лежит на диагонали одного из квадратов и на продолжении диагонали другого.

_{Н. Москвитин}

На отрезке AB выбрана произвольно точка С. На отрезках AC и CB как на сторонах построены квадраты так, что все их вершины лежат по одну сторону от отрезка AB. Постройте с помощью одной линейки квадрат, диагональю которого является отрезок AB.

_{Николай Москвитин}

В квадрате ABCD отмечены середины Е и F двух соседних сторон BC и CD соответственно и проведены прямые AE и BF, пересекающиеся в точке G. Около квадрата описана окружность. Точка пересечения прямой AE с нею- точка H. Доказать: GE=EH.

_{Николай Москвитин}

Если стороны квадрата повернуть вокруг его вершин внутрь квадрата на одинаковый угол, то их взаимопересечения образуют квадрат меньшего размера с тем же центром. Можно ли найти некое аналогичное преобразование для куба? Т.е. поворотом одних элементов куба вокруг других на одинаковый угол высечь во внутреннем пространстве куба куб меньшего объема с тем же центром.

На стороне AD внутри квадрата ABCD построен равносторонний треугольник A’D’E. Треугольник поворачивается так, что его вершина A’ скользит по стороне квадрата от A к D, а вершина D’ скользит по стороне квадрата от D к C. Какую кривую, непрерывно её касаясь, огибает при этом основание A’D’ треугольника? По каким кривым движутся центр O и вершина E треугольника?

Дан квадрат ABCD. Точки K и L являются серединами сторон BC и CD соответственно. Отрезок KD пересекается с диагональю AC и отрезком AL в точках P и Q, соответственно. Найти площадь четырехугольника LQPC, если сторона квадрата равна 60.

_{Альхамов Р.Р.}

На плоскости отмечены 4 точки. Построить квадрат, на сторонах которого лежат эти точки.

Сторона большого квадрата a, найти сторону малого квадрата и радиусы окружностей.

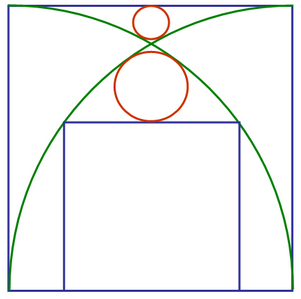
Новогодний подарок от арбузного блога