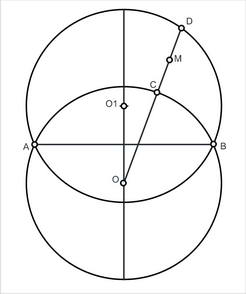
Задача № 258. Заплыв точки по дуге
Четверг, июня 23, 2016Две окружности равного радиуса с центрами в точках О и О1 имеют общую хорду АВ. Из точки О проведен в произвольном направлении отрезок, пересекающий хорду AB, затем пересекающий окружность O в точке С и окружность О1 в точке D. Пусть М – середина отрезка CD. Доказать (или опровергнуть), что геометрическим местом точек M является дуга окружности.