Задача № 267. Касание должно быть легким, но точным.
Вторник, декабря 5, 2017С помощью циркуля и линейки построить окружность, касающуюся двух данных окружностей, причем одной из них в данной точке.
С помощью циркуля и линейки построить окружность, касающуюся двух данных окружностей, причем одной из них в данной точке.
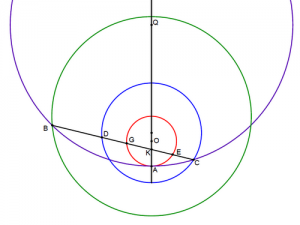
Проведем прямую AQ. С центром в точке O на ней построим окружность диаметром 3 так, что |AO|=1,5 (красная окружность). Отметим на прямой точку K так, что |AK|=1. Проведем через точку K под произвольным углом прямую, пересекающую окружность в точках G и E. Очевидно, в любом случае |GK|*|GE|=2. Построим с центром на прямой AQ окружность диаметром 17, касающуюся первой окружности в точке A (фиолетовая окружность). Пусть прямая GE пересекает вторую окружность в точках B и C. Очевидно, в любом случае |BK|*|CK|=16. Вращая прямую GE вокруг точки K можно найти такое ее положение, что |KE|=2^(1/3), а |GK|=2^(2/3), т.е. |GK|=|EK|^2. Вращая прямую BC вокруг точки K можно найти такое ее положение, что |KC|=2*2^(1/3), а |GE|=4*2^(2/3). С помощью гомотетии с коэффициентом 2 и центром в точке K построим синюю окружность. Точка C пересечения синей и фиолетовой окружности будет обладать замечательным свойством |KE|=|CK|=2^(1/3). Проверим наше построение с помощью окружности, полученной с помощью гомотетии с центром в точке K и коэффициентом 4 (зеленая окружность). На её пересечении с фиолетовой окружностью находится точка B такая, что |BK|=4*|GK|=4*2^(2/3), т.е. |BK|=|CK|^2. Легко убедиться, что точки B, K и E лежат на одной прямой.
Однако, почему не ликуют древние греки? Ведь мы построили отрезок, равный кубическому корню из 2, решив таким образом задачу об удвоении куба! Возможно, в наше построение вкралась ошибка? Найдите её.
На плоскости построены два отрезка длинами a и b. С помощью циркуля и двух прямых углов (например, в виде школьных угольников) построить отрезки длинами c и d — два средних пропорциональных отрезка к данным a и b, т.е. чтобы выполнялось соотношение a:c = c:d = d:b.
В равнобедренном треугольнике ABC AB=BC, угол при вершине B равен 20°. Из вершины A проведена прямая под углом 25° к основанию AC до пересечения со стороной BC в точке E. Из вершины С проведена прямая под углом 65° к основанию AC до пересечения со стороной AB в точке G. Найти угол CGE.
www.gogeometry.com
Дана окружность (центр не отмечен). С помощью только циркуля построить вершины квадрата, вписанного в эту окружность.
Пусть I – центр вписанной окружности остроугольного треугольника ABC, X и Y – точки касания окружности сторон AC и BC соответственно. Через I проведена прямая g, пересекающая стороны AC, BC и окружность в точках K, L, M, N (в таком порядке слева направо). P и Q – основания перпендикуляров, опущенных из точек X и Y на прямую g (точки P и Q находятся внутри окружности).
Доказать, что 1/KL+1/QM=1/MN+1/PL.
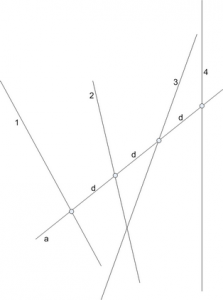
В некой профессии сотни лет решается разными способами следующая задача:
на плоскости имеются 4 прямые общего положения (не параллельны и не проходят через одну точку). Необходимо провести пятую прямую так, чтобы три расстояния между точками ее пересечения с четырьмя исходными прямыми были равны друг другу.
Как бы вы подошли к ее решению? Рассматриваются любые методы: аналитический, графический, с применением любых чертежных инструментов, «точные» и приближенные построения.
В задаче №88 упоминался сюжет задачи 33bis из книги В. И. Арнольда «Задачи для детей от 5 до 15 лет»:
На трех попарно скрещивающихся ребрах куба отмечены точки N, M, Q. Построить сечение куба плоскостью MNQ.
Известно очень интересное дополнительное ограничение к этой задаче:
«… выполняя все построения только на поверхности куба».
незабываемое удовольствие, попробуйте
В треугольник ABC вписана окружность и отмечен её центр I и точки касания P, Q, R со сторонами BC, CA и AB соответственно. Одной линейкой постройте точку K, в которой окружность, проходящая через вершины B и C, касается (внутренним образом) вписанной окружности.
А.Мякишев
На дуге BC описанной окружности равностороннего треугольника ABC расположена точка M. Доказать, что отрезок MA=MB+MC.
Построить прямоугольный треугольник по катету и сумме гипотенузы и другого катета.
На основании AD равнобедренной трапеции ABCD отмечена середина E; вокруг треугольника ABE описана окружность, пересекающая CE в точке F, BF продолжен до пересечения с прямой AD в точке L, около EFL описана окружность с центром Ο. Диаметр её FF1 пересекает прямую AD в точке K, AF пересекает линию симметрии трапеции в точке J. Доказать: JK || BF.
Николай Москвитин
Окружность, построенная на боковой стороне BC равнобедренного треугольника ABC как на диаметре, пересекает высоту AD в точке E. Найти CE, если AC=2.
В треугольнике ABC окружность, построенная на диаметре AC, пересекает высоту BD в точке F, а окружность, построенная на диаметре AB, пересекает высоту CE и её продолжение в точках G и H соответственно. Угол CHF равен 12°. Найти величину угла AGF.
Через середину одной из сторон треугольника провести прямую, делящую периметр треугольника пополам.