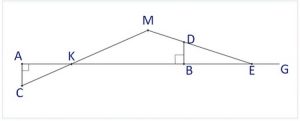
На прямой AG отмечен отрезок AB длиной 2a. Из точек А и B перпендикулярно прямой AG по разные её стороны проведены отрезки AC и BD, причем AC=BD=b.
Из точки C и точки D проведены отрезки СM и DM так, что CM пересекает AB, обозначим точку их пересечения через K, DM пересекает прямую AG вне отрезка AB, обозначим точку их пересечения через E, причем угол MKB равен углу MEB. Найти геометрическое место точек M (составить уравнение кривой).
Метеорит падает на сферическую Землю радиусом R под углом ѳ к отвесу со скоростью V и упруго (без потери энергии) отскакивает. В каком случае (при каком соотношении параметров) метеорит, попрыгав. вернётся в точку падения? (Допустим, g не меняется с высотой).
Е.Скляревский
Из точки, где плоскость, наклоненная под углом α к горизонту, сопрягается с горизонтальной плоскостью, выстрелили шариком под углом β к горизонту. Каким должен быть угол β, чтобы шарик, отскочив от наклонной плоскости, вернулся в точку выстрела?
Е. Скляревский
Пушка стреляет, меняет угол наклона на 1 градус, снова стреляет, пока не обойдет 360 градусов (пушка приподнята над землей). Найти линию, огибающую все траектории снарядов.
Е.Скляревский
Точки A и B подвеса концов невесомого нерастяжимого каната длиной L находятся на неподвижных опорах высотой Ha и Hb, расстояние между основаниями опор по горизонтали равно с. Нетрудно найти траекторию движения канатоходца, идущего по такому канату. Но какова будет траектория движения канатоходца массой m по канату массой M при тех же условиях подвеса каната?
Дан треугольник ABC с длинами сторон BC=a, AC=b, AB=c. Прямые l1 и l2, образующие угол d, делят его на три равновеликие части. Найти геометрическое место вершин угла d.
Николай Москвитин
В горизонтальной плоскости P расположены две взаимно перпендикулярные прямые x и y, пересекающиеся в точке O. В вертикальной плоскости V, перпендикулярной биссектрисе угла между прямыми x и y и содержащей точку O, расположена окружность радиуса a, касающаяся плоскости P в точке O. В плоскости V также расположена концентричная первой окружность радиуса a-1. Окружности, оставаясь вертикальными и концентрическими, начинают перемещаться в направлении биссектрисы угла между x и y так, что большая окружность все время касается прямых x и y. Какую кривую образуют точки пересечения малой окружности с плоскостью P? Найти её уравнение.
Из крана периодически капает вода, капли падают вертикально в воду в бассейне, вертикальная стенка которого находится на расстоянии а от линии падения капель. При падении капля выбивает брызги с поверхности воды. Допустим, брызги разлетаются всегда под углом b к поверхности воды. Какую кривую образуют на стенке бассейна точки падения брызг на неё?
Шарик падает с высоты h на наклонную плоскость и прыгает по ней. Как зависит период прыжков от угла наклона плоскости а? Потерями на трение и соударения пренебречь.
Е.Скляревский
Какую кривую (семейство кривых) описывает в течение года тень верхушки Ташкентской телебашни высотой 375 м?
Е. Скляревский
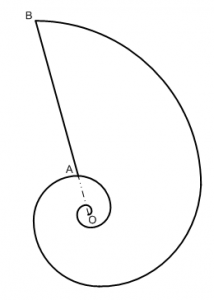
Найти центр тяжести фигуры, ограниченной последним витком логарифмической спирали вида r=ae^(bφ) и отрезком AB радиального луча OB.
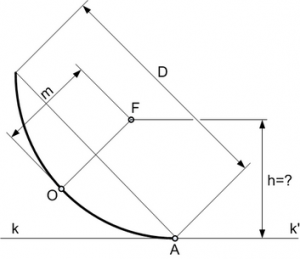
Параболическую антенну диаметром D с фокусным расстоянием OF=m расположили на горизонтальной плоскости kk’ так, что в точке A, принадлежащей диаметру D, парабола касается плоскости kk’. На какой высоте от плоскости kk’ оказался фокус параболы F ?
В кружке диаметром d поверх кофе не смешивающийся с ним слой сливок. На сколько градусов нужно наклонить кружку, чтобы слой сливок стал вдвое тоньше? Какой уровень кофе в кружке должен был быть первоначально, чтобы при требуемом наклоне не обнажилось дно? Какой высоты должна быть кружка, чтобы при требуемом наклоне ни капли сливок не пролилось?
Парабола задана на плоскости фокусом и директрисой. На той же плоскости отмечены произвольно точки P и Q. С помощью циркуля и линейки найти точки пересечения параболы и прямой.
На горизонтальной прямой установлены в вертикальной плоскости, содержащей данную прямую, три окружности радиусов R1, R2 и R3, имеющие общую точку касания между собой и с прямой. Данную точку помечают на прямой как A, на окружностях соответственно A1, A2 и A3. В некоторый момент времени все три окружности начинают катиться по прямой без скольжения в одну сторону с одинаковой для всех трех окружностей и постоянной угловой скоростью w. Доказать, что при этом в любой момент времени точки A, A1, A2 и A3 находятся на одной прямой. Найти зависимость наклона этой прямой к горизонту от времени.
