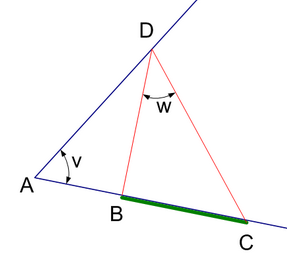
Задача № 101. Параболический треугольник.
Воскресенье, января 10, 2010Составить из дуг парабол криволинейный треугольник наименьшей площади с заданными вершинами (стороны треугольника должны пересекаться только в вершинах и быть направлены выпуклостью внутрь).