Задача № 131. Артразлёт
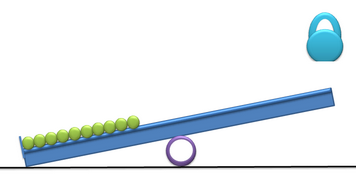
Двухметровая доска лежит на асфальте одним концом, середина доски опирается на трубу. На конце доски буртик, в который упираются уложенные в продольный желобок доски в ряд десять теннисных мячей. Угол наклона доски в первоначальном состоянии 20 градусов к горизонту. На второй конец доски с высоты 1 метр бросают пудовую гирю. На каком расстоянии друг от друга приземлятся мячи?
ноября 8, 2010 - 11:39
http://s011.radikal.ru/i318/1011/1c/2173d24a504d.png — шарики упадут на доску и надо расстояния между ними посчитать?
ноября 9, 2010 - 00:52
ну… вообще-то не факт, что мячи упадут на доску. Задача построена в виде этюда, где решатели самостоятельно делают разные допущения о неоговоренных условиях, таких как упругость доски, ее момент инерции, жесткость трубы, упругость мячей, коэффициенты трения и прочее, самостоятельно оценивают весомость учтенных факторов и т.д. Но дело не в этом, а в конечной закономерности: как будут соотноситься друг с другом дальности полета мячей.
ноября 9, 2010 - 07:23
Ну, допущения сделанные выше стандартные школьные (при которых сделана картинка) — доска невесомая, абсолютно упругая, мячи упругие, труба заменена тонкой точечной опорой, скорость конца доски совпадает со скоростью гири и в момент времени.
Кстати, вот еще подобная задача. Мячик скатывается под действием силы тяжести по обрезанному параболическому трамплину y(x)=(x-a)^2+b — находясь в начальный момент в точке x=0 y=a^2+b, a и b>0 — определить в какой точке обрезать параболу, чтоб дальность полета была максимальной.
ноября 9, 2010 - 23:02
Спасибо! Если не возражаете, Вашу задачу выложу для отдельного рассмотрения: см. № 132.
🙂
марта 26, 2012 - 20:56
Только это не моя задача — это по мотивам задачи с сайта http://www.8foxes.com/