Задачи по геометрии

На стороне AD внутри квадрата ABCD построен равносторонний треугольник A’D’E. Треугольник поворачивается так, что его вершина A’ скользит по стороне квадрата от A к D, а вершина D’ скользит по стороне квадрата от D к C. Какую кривую, непрерывно её касаясь, огибает при этом основание A’D’ треугольника? По каким кривым движутся центр O и вершина E треугольника?

Найти плоскую фигуру наименьшей площади, внутри которой возможен поворот равностороннего треугольника на 360 градусов.

_{Мишаня Дундило}

На вертикально установленной доске в точках A и B закреплены концы нити длиной l > AB. Отрезок AB образует острый угол a с вертикалью. Надетое на нить кольцо в состоянии равновесия находится в точке C. Найти отношение, в котором кольцо делит нить. Массой нити пренебречь. (Рассмотреть два варианта: 1) кольцо свободно скользит по нити; 2) кольцо закреплено на нити.)

_{Из коллекции validolum}

С помощью циркуля и линейки построить четырехугольник со сторонами 2, 3, 4, 5 и углом между диагоналями 60°. Доказать, что центры равносторонних треугольников, построенных на сторонах 2 и 4 с внешней стороны четырехугольника и на сторонах 3 и 5 с внутренней стороны четырехугольника, лежат на одной прямой.

В описанной окружности равнобедренного треугольника ABC (с основанием AC) из вершины B проведена хорда BM. Из вершины C на прямую BM опущен перпендикуляр CH. Прямые AM и CH пересекаются в точке L. Найти геометрическое место точек L при движении точки М по окружности.

_{Форум MathLinks}

В прямоугольном треугольнике ABC с прямым углом при вершине С проведена высота CD. Некоторая точка K в плоскости треугольника находится от вершины A на расстоянии, равном AC, при этом точка O является центром окружности, проходящей через точки A, B, K. Докажите, что отрезок DK перпендикулярен AO.

_{Блог Синаджексона}

ABC – остроугольный треугольник. На стороне AB как на диаметре построили окружность, которая пересекает высоту CC′ и её продолжение в точках M и N. Окружность, построенная на диаметре AC пересекает высоту BB′ и её продолжение в точках P и Q. Докажите, что точки M,N,P,Q лежат на одной окружности.
_{Национальная математическая олимпиада США, 1990}

_{http://www.archimedes-lab.org}

Для любителей начертательной геометрии.

В точках А и В находятся радиолокаторы. Самолет перемещается в направлении t. Определить точки, в которых лучи локаторов будут сходиться к самолету, пересекаясь под прямым углом.

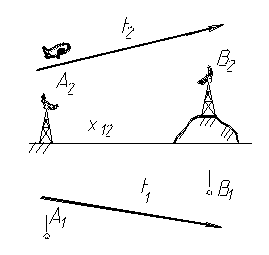
_{из коллекции ЛЭТИ}

Полуостров представляет собой острый угол, внутри которого находится дом лесника. Как леснику, выйдя из дома, добраться до одного берега полуострова, затем до другого и вернуться домой, пройдя при этом по самому короткому пути?

Внутри круга отмечена точка H. Вписать в круг треугольник наименьшей площади с ортоцентром в точке Н.

_{форум братьев по разуму}

На плоскости даны три параллельные прямые. Найдите геометрическое место центров вписанных окружностей треугольников, вершины которых расположены (по одной) на этих прямых.

_{Пятая Всероссийская олимпиада по геометрии}

Построить равносторонний треугольник, одна вершина которого лежала бы на данной оружности, вторая на данной прямой, а третья в данной точке.

_{Б. Делоне, О. Житомирский}

На карте указаны отрезки трёх прямолинейных дорог,
соединяющих три деревни, но сами деревни расположены за пределами
карты. Кроме того, на карте не указана пожарная часть, находящаяся
на равном расстоянии от трёх деревень, хотя место её расположения
находится в пределах карты. Можно ли найти это место с помощью
циркуля и линейки, если проводить построения только в пределах карты?

_{Фольклор}

С помощью циркуля и линейки восстановить треугольник по его описанной окружности и точкам (следам) M, B и H пересечения с ней продолжений медианы, биссектрисы и высоты, опущенных из одной вершины.

_{Из коллекции пользователя Sabit}