Задача № 63. Заливное.
Четверг, июля 16, 2009Лаборант Михалыч вынул пробку, и тут ему позвонили. На столе образовалась лужа глубиной около 1. Оцените форму лужи.
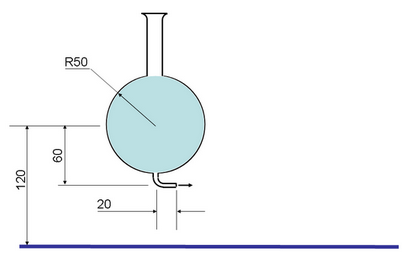
Из объяснительной Михалыча впоследствии выяснилось, что пробка была диаметром 5.
Лаборант Михалыч вынул пробку, и тут ему позвонили. На столе образовалась лужа глубиной около 1. Оцените форму лужи.

Из объяснительной Михалыча впоследствии выяснилось, что пробка была диаметром 5.
Вписать эллипс в заданный параллелограмм.
Проблема любителей AutoCad и не только:)
В описанной окружности равнобедренного треугольника ABC (с основанием AC) из вершины B проведена хорда BM. Из вершины C на прямую BM опущен перпендикуляр CH. Прямые AM и CH пересекаются в точке L. Найти геометрическое место точек L при движении точки М по окружности.
Прямые, проведенные через точку А, касаются окружности с центром О в точках В и С. D — точка пересечения отрезка АО с окружностью. Точка X — основание перпендикуляра, опущенного из точки В на CD. Y — середина отрезка BX. Z — точка пересечения DY с окружностью. Доказать, что угол AZC прямой.
Форум MathLinks
Блок радиусом R укреплен неподвижно и заклинен. В верхнем полюсе блока привязана и пропущена влево веревка длиной L, на конце веревки подвешен груз массой m. Груз отклонили влево так, что веревка отклонилась от вертикали на угол q. Груз отпустили. До какого угла w отклонится от вертикали веревка при движении такого маятника вправо?
Точка Q пересечения диагоналей вписанного в эллипс четырехугольника ABCD делит пополам хорду EF эллипса. EF пересекает стороны AB и CD четырехугольника в точках M и N соответственно. Можно ли доказать, что отрезки MQ и NQ равны?
Бухта представляет из себя острый угол. Найти на левом берегу бухты точку, из которой пляж, расположенный на правом берегу бухты, виден под наибольшим углом.
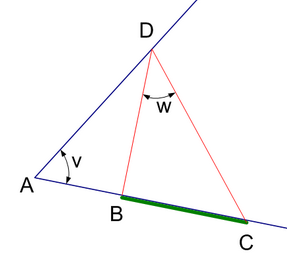
Для любителей начертательной геометрии.
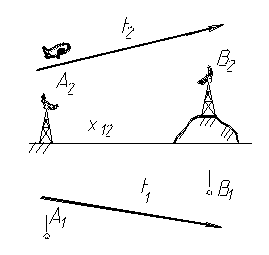
В точках А и В находятся радиолокаторы. Самолет перемещается в направлении t. Определить точки, в которых лучи локаторов будут сходиться к самолету, пересекаясь под прямым углом.
Тонкий обруч массой m и диаметром D установили на горизонтальной плоскости под небольшим углом A к вертикали и катнули, придав начальную скорость v. Какую траекторию опишет точка касания обруча и плоскости до его полной остановки? Коэффициент трения качения обруча по плоскости равен k.
Внутри круга отмечена точка H. Вписать в круг треугольник наименьшей площади с ортоцентром в точке Н.
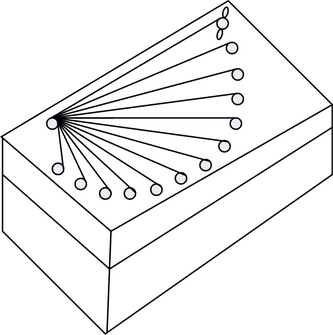
Цветик так красиво играл на флейте, что Незнайка твердо решил составить с ним дуэт и попросил Винтика и Шпунтика изготовить для него гусли, которые настраивались бы всего одной крутилкой, без хитростей и этих там всяких, как их, да, — камертонов, вот. Винтик взял обувную коробку, Шпунтик — рыболовную леску и набор карандашей, и работа закипела. В коробке насверлены отверстия, вставлены карандаши, а леска протянута так, что над крышкой она образует струны, а под крышкой прилегает к ее поверхности и не звучит. Пройдя от первого колка через все остальные, на последнем она подтягивалась и натяжение было одинаковым на всем ее протяжении, что и обеспечивало, собственно, настройку инструмента. Струны издавали звуки хроматической гаммы, т.е. звучали с интервалом в полутон, потому Незнайка гордо назвал новый инструмент «Хромогусли». По какой же системе расположили Винтик и Шпунтик карандаши-колки?
Определите площадь треугольника ММК: Мадрид-Москва-Калькутта.
На карте указаны отрезки трёх прямолинейных дорог,
соединяющих три деревни, но сами деревни расположены за пределами
карты. Кроме того, на карте не указана пожарная часть, находящаяся
на равном расстоянии от трёх деревень, хотя место её расположения
находится в пределах карты. Можно ли найти это место с помощью
циркуля и линейки, если проводить построения только в пределах карты?
Фольклор
Найти полуоси эллипса с фокусами в точках А и С, касающегося прямой f.
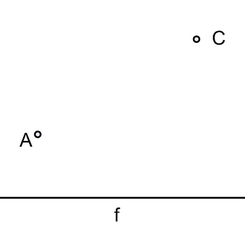
Найти такое положение точки B на прямой f, чтобы сумма отрезков |AB|+|BC| была минимальной.
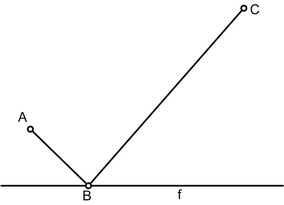
Прислано пользователем Sabit