Архив на категорию ‘Замечательные кривые’
Четверг, сентября 20, 2012
Копытолап убегает по кругу диаметром D со скоростью V. Когтеклюв преследует его со скоростью U, начиная от центра круга и постоянно выдерживая курс точно на копытолапа. По какой траектории движется когтеклюв? При каком минимальном отношении U/V когтеклюв сможет догнать копытолапа? Возможно ли такое соотношение U>V, при котором когтеклюв не догонит копытолапа никогда?
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, Подумалось вдруг, этюды | Нет комментариев »
Четверг, мая 31, 2012
Окружность касается соседних витков логарифмической спирали. Вторая окружность касается тех же двух витков спирали и касается первой окружности внешним образом.Третья касается тех же витков и второй окружности, так далее ряд окружностей продолжается. Доказать или опровергнуть утверждение: отношение диаметров любых двух соседних окружностей в описанном ряду есть величина постоянная для данной логарифмической спирали.
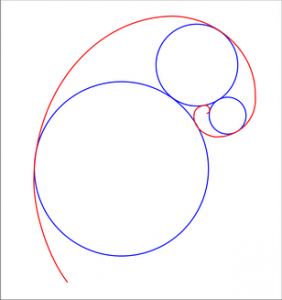
Категория: задачи на доказательство, Замечательные кривые, Подумалось вдруг, этюды | Нет комментариев »
Понедельник, января 16, 2012
Представьте себе куклу-неваляшку. Допустим, ее центр тяжести находится на высоте h над плоскостью опоры. Возможно ли ее нижней поверхности придать такую форму, чтобы время возвращения куклы из наклонного состояния в вертикальное не зависело от угла наклона?
Категория: Замечательные кривые, Механические утехи, около физики, Подумалось вдруг, этюды | Нет комментариев »
Понедельник, октября 31, 2011
Авто поднято на подъемнике. От пола до днища картера 180 см. Ось маслосливной горловины наклонена к вертикали под 45°. На полу оцинкованное ведро посреди кучки опилок. Ловким движением туфли мастер устанавливает ведро так, что при съеме пробки масло точно попадает в ведро, и потом в процессе туфля пододвигает ведро еще пару раз. Можно ли сразу установить ведро так, чтоб пододвигать в процессе не приходилось до полной кончины масла, если высота и диаметр верхнего среза ведра равны 30 см, а глубина масла в картере 10 см?
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, около физики, Парабола, Подумалось вдруг, этюды | Нет комментариев »
Среда, августа 17, 2011
Какую форму приобретёт упругое кольцо, повешенное на гвоздь?
Категория: Замечательные кривые, Механические утехи, Подумалось вдруг, этюды | Нет комментариев »
Вторник, июля 19, 2011
Коля и Петя из хулиганских исследовательских побуждений взяли трубу квадратного сечения за торцы и скрутили, повернув торцы друг относительно друга на 720 градусов. Ось трубы при этом осталась прямолинейной. Трубу прокатили по песку в направлении, перпендикулярном ее оси, слегка придавив её и сделав несколько оборотов, так, что вдоль её траектории не осталось не тронутых трубой участков песка. Попробуйте построить сечения следа на песке в направлении движения трубы и в направлении, параллельном оси трубы.
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, квадрат, Механические утехи, Подумалось вдруг, четырехугольник, этюды | 1 Комментарий »
Четверг, апреля 14, 2011
Антенщик-мачтовик, монтируя что-то там на 500-метровой отметке Останкинской телебашни, выронил гайку. В какую сторону и на сколько метров будет отстоять точка падения гайки на землю от вертикали, проходящей через начальную точку?
фольклор
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, около физики, Парабола | 3 Комментариев »
Среда, апреля 6, 2011
…букашка по имени Жанетта выползла из дырочки в глобусе диаметром 1 метр в точке, обозначающей Кейптаун, и двинулась на северо-восток, строго придерживаясь азимута 45°. Куда она приползёт и какова будет длина её пути?
Старинная задача навигацких наук
Категория: Задачи на вычисление, Замечательные кривые, Классика, на сфере, Преданья старины глубокой, шары | 2 Комментариев »
Вторник, марта 15, 2011
Цилиндрический ролик длиной L и диаметром D катится по горизонтальной плоскости без проскальзываний. В некоторый момент времени диаметр одного из оснований цилиндра начинает меняться пропорционально углу поворота ролика вокруг своей оси (при этом прямолинейность образующей сохраняется, т.е. ролик становится усеченным конусом) и уменьшается за два оборота ролика вокруг своей оси от D до нуля. Какую траекторию опишет на плоскости точка касания малого основания ролика к плоскости?
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, конус, Механические утехи, Подумалось вдруг, этюды | Нет комментариев »
Воскресенье, февраля 27, 2011
Конструкторы нового элеватора из соображений компактности технологической линии в одном месте согнули трубопровод диаметром D со шнеком (архимедовым винтом) внутри в полутор с радиусом по осевой линии R. Шаг винта S по осевой линии остался прежним, диаметр гибкого вала шнека остался равным d, гибкий вал вращался с той же угловой скоростью w, что и вал винта на прямолинейном участке трубопровода. Однако, при испытаниях линии технологи с удивлением обнаружили, что при работе трубопровода с производительностью, приближающейся к N% от максимальной расчетной, возникает… Что же возникает, и возникает ли? А если возникает, то при каком N?
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, Объём, около физики, Подумалось вдруг, этюды | Нет комментариев »
Воскресенье, февраля 20, 2011
Во внутренней полости конуса с вертикальной осью и углом при вершине A на высоте H от вершины конуса вдоль его внутренней поверхности под углом к горизонтали B запускают шарик радиуса r с начальной скоростью v. Трение между конусом и шариком отсутствует, поверхности конуса и шарика абсолютно тверды. Какова будет траектория шарика?
Е.Скляревский
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, конус, Механические утехи, около физики, шары, этюды | 1 Комментарий »
Воскресенье, февраля 20, 2011
По круговым орбитам радиусов R и r с угловыми скоростями u и v вокруг звезды Зю вращаются в одной плоскости планеты Плюк и Шняга. Найти среднее расстояние между планетами.
Е.Скляревский
Категория: Задачи на вычисление, Замечательные кривые, Механические утехи, около физики, шары, этюды | 2 Комментариев »
Вторник, февраля 8, 2011
К вертикальной стороне прямого угла с внутренней стороны примыкает диаметром полуокружность, находящаяся в плоскости этого прямого угла. На полуокружности выбрана произвольная точка С. Нижний конец А диаметра начинает скольжение вдоль горизонтальной стороны угла, а верхний конец B диаметра — вдоль вертикальной стороны угла, при этом полуокружность остаётся в плоскости угла. По какой траектории движется точка С?
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, Механические утехи, Подумалось вдруг | Нет комментариев »
Пятница, декабря 24, 2010
Петя Васильчиков — гениальный ребенок. Так полагает его бабушка Элеонора Бельц. Разумеется, каждый гениальный ребенок просто обязан стать гениальным пианистом. «Только Ronisch 132 !» – настаивала бабушка под самый Новый год. И вот, грузчики Михалыч и Пахомыч пытаются мимо наряженной ёлки закатить пианино в Петину комнату. Для этого им необходимо преодолеть поворот коридора. Ширина коридора до поворота 130 см, длина пианино 152 см, ширина 63 см. Известно, что слегка зацепив обои, но не поцарапав при этом инструмент, грузчики справились с задачей. Какова же была ширина коридора после поворота? Да, интересно также, какой формы следы оставили на полу колеса пианино весом 235 кг.
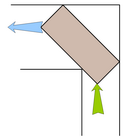
фольклор
Категория: геометрическое место точек, Задачи на вычисление, Замечательные кривые, Механические утехи, Новогодние загадки, этюды | Нет комментариев »
Четверг, декабря 23, 2010
На плоскости начерчены две пересекающиеся окружности радиусов r1 и r2. Можно ли с помощью циркуля и линейки провести третью окружность заданного радиуса r3 так, чтобы она проходила через точку пересечения двух первых и отсекала на них дуги, стягиваемые равными хордами?
Категория: геометрическое место точек, Задачи на построение, Замечательные кривые, Подумалось вдруг, треугольник, этюды | Нет комментариев »

