Задачи по геометрии

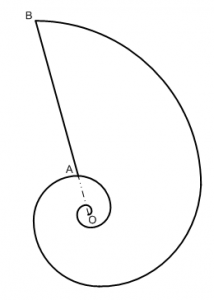
Найти центр тяжести фигуры, ограниченной последним витком логарифмической спирали вида r=ae^(bφ) и отрезком AB радиального луча OB.

В треугольнике ABC с углом B, равным 60 градусам, проведены биссектрисы AA1 и CC1. Срединный перпендикуляр к отрезку A1C1 пересекает прямую AC в точке E. Доказать, что треугольник A1C1E равносторонний.

На плоскости задан отрезок единичной длины. С помощью только циркуля построить фигуру площадью Пи/3+sin(Пи/3).

Через произвольно выбранную на стороне ВС треугольника ABC точку P провести прямую, разбивающую периметр треугольника в заданном отношении m/n. В каких пределах должно находиться отношение m/n, чтобы при данных известных длинах сторон треугольника и данном отношении CP/PB задача имела решение?

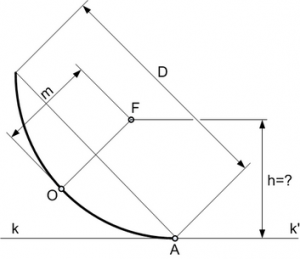
Параболическую антенну диаметром D с фокусным расстоянием OF=m расположили на горизонтальной плоскости kk’ так, что в точке A, принадлежащей диаметру D, парабола касается плоскости kk’. На какой высоте от плоскости kk’ оказался фокус параболы F ?

Через произвольно отмеченную на стороне треугольника точку провести прямую, делящую площадь треугольника в заданном отношении m/n.

На ребре AD тетраэдра ABCD произвольно отмечена точка P. Построить сечение тетраэдра плоскостью, проходящей через точку P и делящей его объем 1) пополам; 2) в заданном отношении m/n.

В герметичном тонкостенном сосуде, имеющем форму усеченной пирамиды, находится вода. Когда сосуд устанавливают на большее основание площадью S, уровень воды составляет 40% высоты сосуда. Когда же сосуд переворачивают и устанавливают на меньшее основание площадью s, уровень воды составляет 50% высоты сосуда. Какую часть объема сосуда занимает вода? Можно ли определить отношение S/s ?

Парабола задана на плоскости фокусом и директрисой. На той же плоскости отмечены произвольно точки P и Q. С помощью циркуля и линейки найти точки пересечения параболы и прямой.

Уважаемые посетители, сайту geom.uz исполнилось 4 года. Есть повод подвести итоги. Буду рад услышать ваши отклики, предложения, замечания. Пишите сюда в комментарии или на geomuz[at]yandex.ru ! Присылайте оригинальные задачи!
🙂

На горизонтальной прямой установлены в вертикальной плоскости, содержащей данную прямую, три окружности радиусов R1, R2 и R3, имеющие общую точку касания между собой и с прямой. Данную точку помечают на прямой как A, на окружностях соответственно A1, A2 и A3. В некоторый момент времени все три окружности начинают катиться по прямой без скольжения в одну сторону с одинаковой для всех трех окружностей и постоянной угловой скоростью w. Доказать, что при этом в любой момент времени точки A, A1, A2 и A3 находятся на одной прямой. Найти зависимость наклона этой прямой к горизонту от времени.

«Увидел Садко: во синем море
Стоит палата белокаменная.»

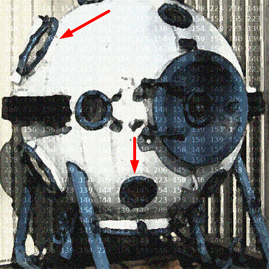
Лампа внутреннего освещения в батисфере диаметром D расположена в её верхней полюсной точке. В боковой поверхности верхней полусферы имеется круглый иллюминатор диаметром d1, а в боковой поверхности нижней полусферы — диаметром d2. Ось верхнего иллюминатора наклонена под 45° к горизонту, а нижнего — под 60°. Батисфера встала на горизонтальном участке дна на шасси так, что нижняя полюсная точка сферы оказалась на высоте h над дном. Какую форму и размеры будут иметь световые пятна на дне от лучей, проходящих через иллюминаторы?
Толщиной стенок, преломлением, рефракцией и рассеянием света Садко пренебрег, ну и мы тоже.

Диагонали произвольного вписанного четырехугольника ABCD пересекаются в точке P. Доказать, что AB*BC*PD=AD*DC*PB.

В основании пирамиды высотой h лежит правильный треугольник со стороной а. Найти соотношение, в котором находятся двугранные углы при основании пирамиды.

Копытолап убегает по кругу диаметром D со скоростью V. Когтеклюв преследует его со скоростью U, начиная от центра круга и постоянно выдерживая курс точно на копытолапа. По какой траектории движется когтеклюв? При каком минимальном отношении U/V когтеклюв сможет догнать копытолапа? Возможно ли такое соотношение U>V, при котором когтеклюв не догонит копытолапа никогда?