Прямые, проведенные через точку А, касаются окружности с центром О в точках В и С. D — точка пересечения отрезка АО с окружностью. Точка X — основание перпендикуляра, опущенного из точки В на CD. Y — середина отрезка BX. Z — точка пересечения DY с окружностью. Доказать, что угол AZC прямой.
Форум MathLinks
В прямоугольном треугольнике ABC с прямым углом при вершине С проведена высота CD. Некоторая точка K в плоскости треугольника находится от вершины A на расстоянии, равном AC, при этом точка O является центром окружности, проходящей через точки A, B, K. Докажите, что отрезок DK перпендикулярен AO.
Блог Синаджексона
ABC – остроугольный треугольник. На стороне AB как на диаметре построили окружность, которая пересекает высоту CC′ и её продолжение в точках M и N. Окружность, построенная на диаметре AC пересекает высоту BB′ и её продолжение в точках P и Q. Докажите, что точки M,N,P,Q лежат на одной окружности.
Национальная математическая олимпиада США, 1990
Блок радиусом R укреплен неподвижно и заклинен. В верхнем полюсе блока привязана и пропущена влево веревка длиной L, на конце веревки подвешен груз массой m. Груз отклонили влево так, что веревка отклонилась от вертикали на угол q. Груз отпустили. До какого угла w отклонится от вертикали веревка при движении такого маятника вправо?
Точка Q пересечения диагоналей вписанного в эллипс четырехугольника ABCD делит пополам хорду EF эллипса. EF пересекает стороны AB и CD четырехугольника в точках M и N соответственно. Можно ли доказать, что отрезки MQ и NQ равны?
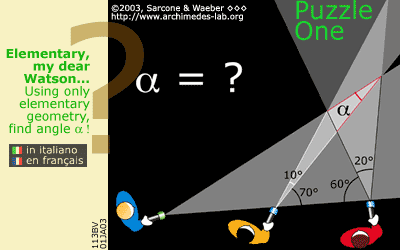
Бухта представляет из себя острый угол. Найти на левом берегу бухты точку, из которой пляж, расположенный на правом берегу бухты, виден под наибольшим углом.
Шарик для настольного тенниса (m=2,7 г, R=20 мм) заполнен наполовину растительным маслом (плотностью p=0,9 г/см^3) и опущен в пустой цилиндрический стакан радиуса 25 мм. Сколько воды нужно налить в стакан, чтобы шарик перестал опираться на дно стакана?
Для любителей начертательной геометрии.
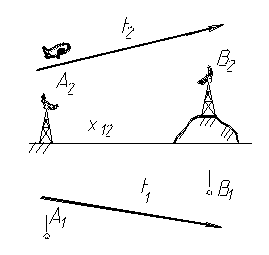
В точках А и В находятся радиолокаторы. Самолет перемещается в направлении t. Определить точки, в которых лучи локаторов будут сходиться к самолету, пересекаясь под прямым углом.
Тонкий обруч массой m и диаметром D установили на горизонтальной плоскости под небольшим углом A к вертикали и катнули, придав начальную скорость v. Какую траекторию опишет точка касания обруча и плоскости до его полной остановки? Коэффициент трения качения обруча по плоскости равен k.
Полуостров представляет собой острый угол, внутри которого находится дом лесника. Как леснику, выйдя из дома, добраться до одного берега полуострова, затем до другого и вернуться домой, пройдя при этом по самому короткому пути?
Внутри круга отмечена точка H. Вписать в круг треугольник наименьшей площади с ортоцентром в точке Н.
На плоскости даны три параллельные прямые. Найдите геометрическое место центров вписанных окружностей треугольников, вершины которых расположены (по одной) на этих прямых.
Построить окружность, проходящую через данную точку и касательную к двум данным окружностям.
Имеются два одинаковых больших шара радиуса R, два одинаковых малых шара радиуса r, весьма длинный цилиндр радиуса p и плоскость. Всего шесть предметов. Как они расположены в пространстве – не сказано, но известно, что каждый из этих шести предметов касается остальных пяти, причем цилиндр касается плоскости по образующей, а шаров – боковой поверхностью. Зная радиус r малых шаров, найти радиусы R больших шаров и p цилиндра.
Б. Делоне, О. Житомирский
