На плоскости имеются окружность и прямая произвольного положения. На прямой отмечена точка А. Построить окружность, касающуюся данной окружности и касающуюся данной прямой в точке А.
Из коллекции пользователя Sabit
С помощью циркуля и линейки построить на плоскости радиус данного шара.
Параболу у=(1/360)х2 повернули на (1/360)° вокруг начала отсчёта. Пересечёт ли она положительную полуось ординат?
Построить правильный 5-угольник по 5 точкам на его сторонах.
Задача предложена Jan в комментариях к задаче № 22.
Через две фиксированные точки O и O1 проведены параллельные прямые f и g. Через точку О проведена прямая, перпендикулярная к ним, до пересечения с g в точке C, через C проведена прямая, перпендикулярная к OO1 до пересечения с f в точке M. Что являет собой геометрическое место точек M? Можете ли дать уравнение?
Оценить отношение ширины полосы к ее длине, при котором цилиндр, склеенный из этой полосы, можно вывернуть наизнанку не деформируя. (Материал вроде бумаги, под деформацией имеются в виду сгибы, складывание, разрывы и т.д.)
источник
Известна теорема Мансиона:
Отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
Рискнем распространить ее на пространственные формы:
Отрезок, соединяющий центры вписанной и вневписанной сфер тетраэдра, делится описанной сферой пополам.
Докажите или опровергните.
На плоскости отмечены 4 точки. Построить квадрат, на сторонах которого лежат эти точки.
Сторона большого квадрата a, найти сторону малого квадрата и радиусы окружностей.
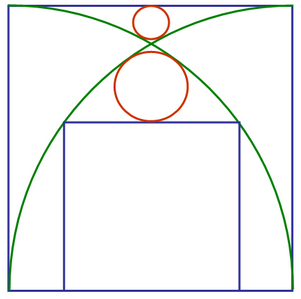
Новогодний подарок от арбузного блога
Для данной хорды MN окружности рассматриваются треугольники ABC, основания которых являются диаметрами этой окружности, не пересекающие MN, а стороны АС и BC проходят через концы M и N хорды MN. Докажите, что высоты всех таких треугольников ABС, опущенные из вершины C на сторону AB, пересекаются в одной точке.
Квант. М1276. Е. Куланин
В колодец опущены две тростинки, одна длиной 2 меры, другая — 3 меры. Тростинки скрещиваются на высоте 1 меры над дном колодца. Каков диаметр колодца?
Через произвольную точку внутри сферы проведены три взаимно перпендикулярные хорды, разбитые данной точкой на отрезки a и b, c и d, e и f соответственно. Найти радиус сферы.
Два цилиндра диаметром 1 пересекаются под прямым углом. Найти объем общей части цилиндров.
В равносторонний треугольник вписана окружность. Докажите, что сумма квадратов расстояний от вершин треугольника до произвольно взятой точки на окружности — величина постоянная.
Чарлз Тригг. Задачи с изюминкой. М., «Мир», 1975.
