Задачи по геометрии

Старинная задача от Мартина Гарднера
Через центр шара просверлено сквозное круглое отверстие длиной 6 см. Найти объем оставшейся части шара.

Основанием наклонной пирамиды является неправильный пятиугольник ABCDE. На основании, касаясь его в точке P лежит шар радиуса R, касающийся всех боковых рёбер пирамиды. Снизу в точке Q основания касается второй шар радиуса 2R, касается он и продолжений всех боковых рёбер пирамиды. Расстояние между центрами шаров равно 4R. Найти сумму расстояний |PC| и |QC|.

Старая загадка от Мартина Гарднера.
В зеркале вы видите свои колени. Чтобы увидеть свои ботинки, нужно подойти к зеркалу или отойти?
🙂

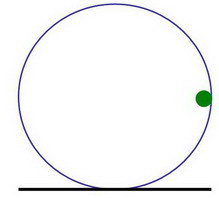
На горизонтальной плоскости стоит вертикально тонкое кольцо радиуса R. Масса кольца M. С внутренней стороны кольцо имеет канавку, по которой может кататься без трения шарик радиуса r массой m. Шарик располагают в канавке в правой полюсной точке кольца и отпускают. Коэффициент трения качения кольца по плоскости равен k. Как далеко и в какую сторону укатится кольцо? По какой траектории будет двигаться шарик в неподвижной системе координат?

Хорошо забытое старое

Три шара разных диаметров лежат на плоскости, касаясь друг друга. Сверху их касется другая плоскость. Найти угол между плоскостями.

Тараканы решили устроить новогодние бега по ленте Мёбиуса. Расчертили на ней 8 дорожек, провели линию старта, договорились, что она же будет и линией финиша, и побежали. По какой дорожке финиширует стартовавший по третьей дорожке?

Вариация на тему задачи №5.
Прямой угол поворачивается вокруг эллипса, неотрывно касаясь эллипса обеими сторонами. Какую кривую описывает вершина угла?

Имеется круг, вырезанный из листа бумаги. На нём отмечена точка, отличная от центра. Изобразите на круге эллипс.

В чёрной-чёрной комнате на чёрной-чёрной стене висят чёрные-чёрные часы. Длина часовой стрелки составляет половину минутной. Ровно в 12 часов концы часовой и минутной стрелки соединили натянутой резиновой нитью. Какую кривую опишет середина нити до следующей встречи стрелок?

Построить вписанную окружность сферического треугольника.

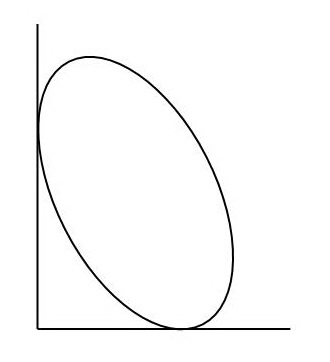
Эллипс поворачивается, касаясь обеих сторон прямого угла. Какую кривую описывают фокусы эллипса? По какой линии перемещается центр эллипса? Какую кривую описывает точка пересечения нормалей к эллипсу, проведенных через точки касания сторон угла? А если угол не прямой?

Построить треугольник по стороне а, медиане m и радиусу R  описанной окружности.

Можно ли эллипс с эксцентриситетом е установить на плоскости, наклоненной под углом w к горизонту, так, что эллипс останется неподвижен?

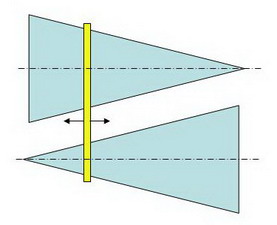
Всем знакомый с детства вариатор. Два конических вала, ремень… Изменяется ли натяжение ремня при его перемещении? Если да, то какой формы должны быть валы (вместо конических), чтобы натяжение (соответственно и длина) ремня оставалось постоянным?