Дата: марта 10, 2011 Автор: balu
Кубики можно складывать в столбики. Об этом любой пацак знает. Добрые четлане конечно вернут Вас на Землю, вот только если задачку решите: перед Вами 15 одинаковых с виду кубиков. Если индикатор направить на столбик пацакских кубиков, на нём загорится зеленая лампочка, но если в столбике есть хоть один четланский кубик, индикатор засветится оранжевым. Известно, что среди 15 кубиков два четланские, а остальные пацакские. Четлане предлагают найти оба четланских кубика, использовав индикатор не более 7 раз. И Вы дома. На Земле. Ну, а не найдете, сами понимаете — транфлюкатор…
старинная четланская загадка
Дата: февраля 27, 2011 Автор: balu
Конструкторы нового элеватора из соображений компактности технологической линии в одном месте согнули трубопровод диаметром D со шнеком (архимедовым винтом) внутри в полутор с радиусом по осевой линии R. Шаг винта S по осевой линии остался прежним, диаметр гибкого вала шнека остался равным d, гибкий вал вращался с той же угловой скоростью w, что и вал винта на прямолинейном участке трубопровода. Однако, при испытаниях линии технологи с удивлением обнаружили, что при работе трубопровода с производительностью, приближающейся к N% от максимальной расчетной, возникает… Что же возникает, и возникает ли? А если возникает, то при каком N?
Дата: февраля 26, 2011 Автор: balu
…через данную точку вне окружности провести касательную к этой окружности.
Дата: февраля 20, 2011 Автор: balu
Во внутренней полости конуса с вертикальной осью и углом при вершине A на высоте H от вершины конуса вдоль его внутренней поверхности под углом к горизонтали B запускают шарик радиуса r с начальной скоростью v. Трение между конусом и шариком отсутствует, поверхности конуса и шарика абсолютно тверды. Какова будет траектория шарика?
Е.Скляревский
Дата: февраля 20, 2011 Автор: balu
По круговым орбитам радиусов R и r с угловыми скоростями u и v вокруг звезды Зю вращаются в одной плоскости планеты Плюк и Шняга. Найти среднее расстояние между планетами.
Е.Скляревский
Дата: февраля 16, 2011 Автор: balu
Продолжения биссектрис треугольника ABC пересекают его описанную окружность в точках D, E, F. Пусть K, L, M — точки пересечения сторон треугольника DEF с биссектрисами треугольника ABC . Доказать, что продолжения отрезков KL, LM и KM отсекают от треугольника ABC три ромба.
Н. Москвитин
Дата: февраля 12, 2011 Автор: balu
Дорогая редакция!
Пишет вам Петя Пробиркин из секретной химической лаборатории Спецсредмашпоставки города N-ска. В нашей лаборатории я служу программистом робототехники. Роботы наши в герметически закрытом помещении переливают и смешивают ядовитые реактивы. Сосуды используются при этом старинные: чашки Петри, колбы, стаканы, пробирки, мензурки, реторты и т.д. Сосуды цилиндрические, конические, полусферические, сферические. Передо мной поставили задачу запрограммировать роботов определенным образом. Для каждой пары изливающего и приемного сосудов разной формы робот должен выбирать такой закон изменения угла наклона изливающего сосуда от времени, чтобы уровень жидкости в приемном сосуде рос с постоянной скоростью. Вязкостью и поверхностным натяжением разрешили пренебречь. Помогите, люди добрые, алгоритмами!
Дата: февраля 8, 2011 Автор: balu
К вертикальной стороне прямого угла с внутренней стороны примыкает диаметром полуокружность, находящаяся в плоскости этого прямого угла. На полуокружности выбрана произвольная точка С. Нижний конец А диаметра начинает скольжение вдоль горизонтальной стороны угла, а верхний конец B диаметра — вдоль вертикальной стороны угла, при этом полуокружность остаётся в плоскости угла. По какой траектории движется точка С?
Дата: февраля 4, 2011 Автор: balu
Внутри данного угла выбрана произвольная точка P. С центром в точке P проведена окружность радиусом R. Можно ли с помощью циркуля и линейки провести касательную к этой окружности так, что точка касания делила бы пополам отрезок, отсекаемый от касательной сторонами угла?
Дата: января 27, 2011 Автор: balu
В треугольнике ABC проведены высоты AD и BE, пересекающиеся в точке H. G — середина стороны AB. Прямые AB и DE пересекаются в точке F. Докажите, что прямые CF и GH перпендикулярны.
dxdy.ru
Дата: января 25, 2011 Автор: balu
Около равнобедренного треугольника ABC с основанием AC описана окружность. В треугольнике проведены все высоты. Точка их пересечения F. Высота CE продолжена до пересечения с данной окружностью в точке G. Около треугольника GBF описана окружность. Доказать, что высота AD является касается второй окружности в точке F.
Н. Москвитин
Дата: января 14, 2011 Автор: balu
Меньшее основание BC трапеции ABCD относится к большему основанию AD как 1:2. В трапеции проведена высота DE к боковой стороне AB.
Доказать: CE=CD
Н. Москвитин
Дата: января 12, 2011 Автор: balu
На окружности радиуса R отмечены последовательно точки A, B, C, D, M. На дугу AB опирается угол α, на дугу BC — угол β, на дугу CD — угол γ. Ломаную вдоль хорд ABCD выполнили из проволоки постоянного сечения и установили точкой C на рычажные весы V. Если α и β известны, при каком угле γ проволока будет находиться в равновесии? Зависит ли γ от R?
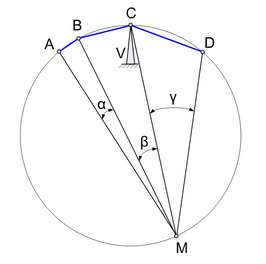
Дата: января 11, 2011 Автор: balu
На отрезке AG произвольно выбрана точка D и на полученных отрезках как на сторонах построены квадраты ABCD и DEFG с вершинами по одну сторону от отрезка. Доказать, что середина отрезка BF лежит на диагонали одного из квадратов и на продолжении диагонали другого.
Н. Москвитин
Дата: января 6, 2011 Автор: balu
На стороне остроугольного треугольника обнаружить такую точку M, из которой луч света, пущенный под некоторым углом, отразившись последовательно от двух других сторон треугольника, вернулся бы в исходную точку M.
