На плоскости лежат, касаясь друг друга, два шара радиусов R и r. Найти геометрическое место центров шаров, касающихся двух данных. Интересно составить уравнение кривой пересечения ГМТ с опорной плоскостью шаров. Если ГМТ разбивает пространство на два полупространства, можно ли оценить отношение частей объема «меньшего» из них, на которые разбивает его опорная плоскость?
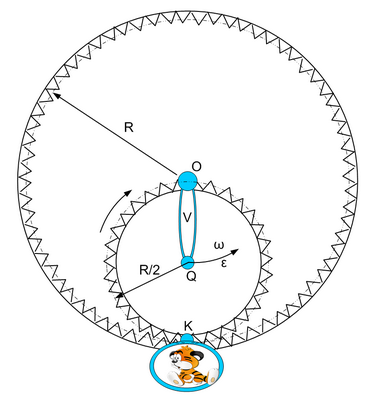
В большом неподвижном колесе R водило V длиной R/2 начинают вращать вокруг центра O с угловым ускорением ε до поворота его на 180 градусов, после чего вращение замедляют с тем же ускорением до остановки его в начальной точке. При этом малое колесо R/2, ось вращения которого находится на конце водила в точке Q, катится по большому благодаря зубчатому зацеплению. В точке контакта колес перед началом движения K на оси, расположенной на малом колесе, подвешена (с возможностью вращения вокруг этой оси) спецлюлька, куда инкапсулирован космонавт. Какую максимальную перегрузку испытает космонавт?
в процессе испытаний все были пристегнуты ремнями безопасности, и никто не пострадал
На чертеже имеются две прямые, точка пересечения которых лежит за пределами чертежа, и произвольная точка P. Необходимо с помощью односторонней линейки построить прямую, проходящую через точку P и точку пересечения данных прямых.
На плоскости даны прямая и точка, не лежащая на этой прямой. Необходимо опустить из точки перпендикуляр на прямую с помощью односторонней линейки и циркуля, причем циркулем можно воспользоваться только один раз, для того чтобы нарисовать дугу/окружность или сделать засечки (с одним центром, не меняя радиус).
JH со ссылкой на фольклор НГУ
В горизонтальной плите имеется лунка в форме полусферы радиусом R. Тонкий стержень длиной L лежит одним концом в лунке, второй конец торчит. Трение между стержнем и лункой отсутствует. Найти угол стержня к горизонту.
Форум СПбГУ
На плоскости заданы произвольный отрезок AB и отрезок единичной длины. С помощью циркуля и линейки разделить отрезок AB на два отрезка так, чтобы отношение одного из них к единице было равно отношению второго к первому.
На стороне AD ромба ABCD взята точка M. Доказать, что окружности, вписанные в треугольники ABM, BMC и CMD, имеют общую касательную.
О.П. Зеленяк
Доказать, что если точку пересечения касательных к эллипсу в концах хорды, содержащей фокус, соединить с этим фокусом, получившаяся прямая будет перпендикулярна хорде.
А. В. Акопян, А. А. Заславский
Вот среди ночи тайком взяли Вы, к примеру, конус из детского набора деревянных фигур и из баловства, ну вот буквально от нечего делать, не задумываясь, начертили у него на боку циркулем «окружность». Ну и конечно же заметили, что окружность какая-то не круглая. И на развертке конуса не круглая. И вообще никак не круглая. И решили составить уравнение этой кривулины на развертке конуса. Вот и мучайтесь! Да. А я спать пошел. 🙂
Можно ли одним раствором циркуля построить на листе бумаги кривую вида
y=b(1-((a/b)Sin(x/a))^2)^0,5
?
Солнце в зените. На горизонтальной плоскости стоит вертикально круглый тонкий обруч диаметром D. Обруч начинает падать. Тень от обруча превращается в эллипс. Вы надеваете волшебные очки и видите, как сближаются фокусы эллипса. Шмяк! Обруч улегся горизонтально, фокусы слились в центре, волшебство исчезло. Допустим, обруч заваливался на бок с постоянной угловой скоростью w. Каков же был закон сближения (относительного движения) фокусов? А если обруч потерял равновесие и падал на бок под действием силы тяжести?
Две окружности касаются между собой в точке М, а радиусы окружностей различаются в полтора раза. Проведем диаметры АМ и ВМ. Известно, что длина отрезка АВ на 4 см больше радиуса одной из окружностей и на 6 см больше радиуса другой из окружностей.
Найти радиусы окружностей.
Математический фольклор. Задача предложена Шухратом Исмаиловым на конкурсе «Учитель года-2010»
Дан отрезок AB, на котором выбрана точка L. Найти геометрическое место вершин С треугольников ABC, для которых CL — биссеткриса угла ACB.
Через центр O вписанной в треугольник ABC окружности проведена прямая, перпендикулярная прямой AO и пересекающая прямую BC в точке M. Из точки O на прямую AM опущен перпендикуляр OD. Докажите, что точки A, B, C и D лежат на одной окружности.
Мотоциклист поднимается в гору от точки А к точке В. Путь его пролегает в вертикальной плоскости, проходящей через точки А и В. Сила тяги двигателя мотоцикла постоянна. При какой форме склона горы мотоциклист преодолеет свой путь за кратчайшее время? Масса вместе с мотоциклом M, скорость V в точке A максимальна для развиваемой двигателем тяги F, скольжение отсутствует.
