Дано: треугольник ABC. Известно, что высота BD образует со стороной BC угол в 45 градусов. Считается, что прямая BD, содержащая высоту, уже построена. Как всего одним движением циркуля построить ортоцентр треугольника ABC?
Николай Москвитин
Дана равнобедренная трапеция. Доказать следующие утверждения:
1)Точки пересечения прямых, проходящих через вершины тупых углов трапеции и образующих (попарно) равные углы одна с верхним основанием, другая с боковой стороной трапеции, и вершины тупых углов лежат на одной окружности.
2)Центр этой окружности лежит на пересечении перпендикуляров к боковым сторонам трапеции, проходящих через эти вершины, причём угол, образуемый этими прямыми, в два раза больше осторого угла трапеции. (аналогичные утверждения можно вывести для другого основания с той оговоркой, что во втором утверждении указанный угол будет больше 180 градусов.)
Николай Москвитин
Радиус купола R, коэффициент трения лапок птиц о купол k. Сколько птиц поместится на куполе, если одна птица занимает площадь S? Еще надо уточнить, что птички — неделимые, недеформируемые кружки площадью S.
Е.С. Скляревский Компот
Мячик скатывается под действием силы тяжести по обрезанному параболическому трамплину y(x)=(x-a)^2+b — находясь в начальный момент в точке x=0 y=a^2+b, a и b>0 — определить в какой точке обрезать параболу, чтоб дальность полета была максимальной.
YuK
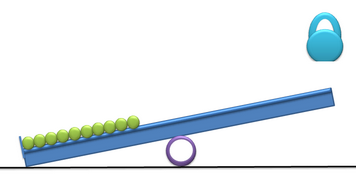
Двухметровая доска лежит на асфальте одним концом, середина доски опирается на трубу. На конце доски буртик, в который упираются уложенные в продольный желобок доски в ряд десять теннисных мячей. Угол наклона доски в первоначальном состоянии 20 градусов к горизонту. На второй конец доски с высоты 1 метр бросают пудовую гирю. На каком расстоянии друг от друга приземлятся мячи?
Имеется тонкостенная коническая колба диаметром у основания 100 мм, углом при вершине конуса 90 градусов, с цилиндрическим горлышком диаметром 20 мм. В колбу пропихнули эластичный резиновый шарик диаметром 50 мм и плотностью 0,5 г/см^3. Колбу затем наполнили водой и опрокинули. Сколько воды останется в колбе, если при касании шариком стенки колбы или её горлышка, он запирает собой отверстие?
Вписать в остроугольный треугольник ABC треугольник KLM минимального периметра (с вершинами K на AB, L на BC, M на CA).
В.И. Арнольд
Найти внутри данного треугольника АВС такую точку T, что площади треугольников АTС, ВTС и АTВ относятся, как n : m : k.
Из вершин треугольника проведены прямые, каждая из которых делит противоположную сторону в отношении m/n. Найти площадь треугольника, образованного взаимным пересечением этих трех прямых.
старинная арбузная тема
Суммарный объем двух кубиков равен 17. Не могли бы Вы указать их точные размеры?
По следам Домашнего задания
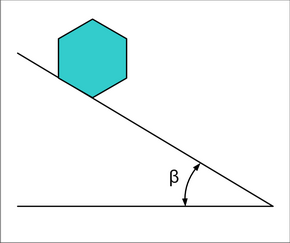
На плоскость, наклоненную к горизонту под углом бета, кладут монолитную шестигранную прямоугольную призму так, что её продольная ось параллельна горизонту, и отпускают. Случись покатившейся призме подпрыгнуть или, приземлившись, удариться о плоскость, удар будет абсолютно упругим. Скольжение между плоскостью и призмой отсутствует. Найдется ли такой угол бета, при котором покатившаяся и ненароком оторвавшаяся от плоскости призма приземлится на наклонную плоскость точно какой-либо из своих боковых граней (ну то есть не ударится о неё ребром, высекая искры, а шлёпнется всей боковой гранью плашмя)?
Внутри окружности выбраны произвольно две точки A и B. Найти такое направление луча из точки A, чтобы отраженный от окружности луч попал в точку B.
Угол при вершине B треугольника ABC составляет 120 градусов. Продолжение биссектрисы угла B пересекает описанную окружность треугольника в точке L. Докажите, что BL= AB + BC.
Вавилонская башня. По боковой поверхности конуса винтовая лестница. При постоянном шаге винта угол подъема лестницы по мере приближения к верхушке башни увеличивается. А можно ли построить сужающуюся кверху башню такой формы, чтобы и шаг винта лестницы был постоянным, и угол её подъема сохранялся одинаковым от подножья до верхушки?
На плоскости начерчен угол и точка P внутри угла. Кроме того, вне угла имеется отрезок AB. Можно ли с помощью циркуля и линейки построить проходящий через точку P отрезок длиною AB, концы которого лежат на сторонах угла?
