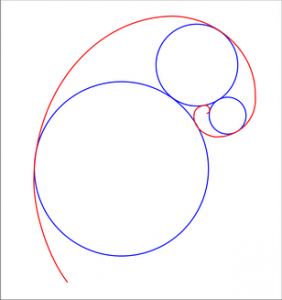
Задача № 195. Неуместившаяся окружность
Воскресенье, июня 24, 2012В равностороннем треугольнике ABC окружность O касается стороны AC в точке T, а стороны AB и BC пересекает в точках D,E и F,G соответственно. Доказать, что AT + BD + BE = CT + BF + BG.